洛谷——搜索

1.洛谷 P1019 单词接龙

题目描述

单词接龙是一个与我们经常玩的成语接龙相类似的游戏，现在我们已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”（每个单词都最多在“龙”中出现两次），在两个单词相连时，其重合部分合为一部分，例如 beast和astonish，如果接成一条龙则变为beastonish，另外相邻的两部分不能存在包含关系，例如at 和 atide 间不能相连。

输入输出格式

输入格式：

输入的第一行为一个单独的整数n (n<=20)表示单词数，以下n 行每行有一个单词，输入的最后一行为一个单个字符，表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在.

输出格式：

只需输出以此字母开头的最长的“龙”的长度

输入输出样例

输入样例#1：

5
at
touch
cheat
choose
tact
a

输出样例#1：

23           （连成的“龙”为atoucheatactactouchoose）   

说明

NOIp2000提高组第三题

思路：

　　输入之后要先检查能不能接龙，如果能进行dfs，搜索最长的龙

(⊙v⊙)嗯~ 代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n,maxn,idx[25];
char first;
char word[25][100];
int lian[25][25];//0为不能连接，否则为能连接，最大连接长度 
bool check(int i,int j,int pos,int l1,int l2)   //检查能否将i的后半部分与j的前半部分接起来 
{         //两个字符串，i接的起点，两个字符串的长度 
    if(l1-pos>=l2)return false;   //>：一定不能接，=：就算能接也单词之间包含 
    for(int k=pos,h=0;k<l1;k++,h++)if(word[i][k]!=word[j][h])return false;//不匹配 
    return true;
}
int dfs(int i)
{ 
    int num=0;//从i开始的最长长度 
    for(int j=1;j<=n;j++)
    {
        if(lian[i][j] && idx[j]<2){idx[j]++;num=max(num,dfs(j)+lian[i][j]);idx[j]--;}
    }     //可连接，注意不能等于2，因为马上就要idx++，就是3了 
    return num;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%s",word[i]);
    do{scanf("%c",&first);} while(!isalpha(first)); //读入字母，小心读入‘
’ 
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
      {          
          int l1=strlen(word[i]),l2=strlen(word[j]);
          for(int pos=l1-1;pos>0;pos--) //pos>0而非>=的原因：单词不能有包含关系 
              if(check(i,j,pos,l1,l2)){lian[i][j]=l2-(l1-pos);break;}//这个lian是把j接在i后j的长度 
      }                                          //break：贪心，接的部分越少则总长度越长 
    for(int i=1;i<=n;i++)if(word[i][0]==first)
    {
        idx[i]++; 
        maxn=max(maxn,(int)strlen(word[i])+dfs(i)); 
        idx[i]--;  //不要忘了减回来 
    }
    cout<<maxn<<"
";    
    return 0;
}

2.洛谷 P1034 矩形覆盖

题目描述

在平面上有 n 个点（n <= 50），每个点用一对整数坐标表示。例如：当 n＝4 时，4个点的坐标分另为：p1（1，1），p2（2，2），p3（3，6），P4（0，7），见图一。

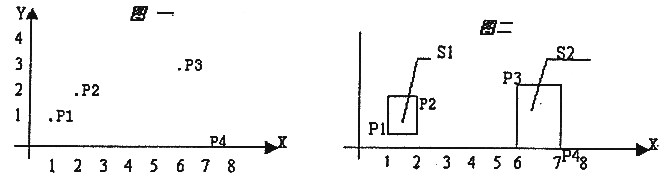
这些点可以用 k 个矩形（1<=k<=4）全部覆盖，矩形的边平行于坐标轴。当 k=2 时，可用如图二的两个矩形 sl，s2 覆盖，s1，s2 面积和为 4。问题是当 n 个点坐标和 k 给出后，怎样才能使得覆盖所有点的 k 个矩形的面积之和为最小呢。约定：覆盖一个点的矩形面积为 0；覆盖平行于坐标轴直线上点的矩形面积也为0。各个矩形必须完全分开（边线与顶点也都不能重合）。

输入输出格式

输入格式：

n k xl y1 x2 y2 ... ...

xn yn （0<=xi,yi<=500)

输出格式：

输出至屏幕。格式为：

一个整数，即满足条件的最小的矩形面积之和。

输入输出样例

输入样例#1：

4 2
1 1
2 2
3 6
0 7

输出样例#1：

4
思路：

　　最最保险的做法：dfs+剪枝，当k>=4时也能做。

　　原则：枚举每一个点，可以任意加入到k个矩形中的某一个，从而得到最优解。

　　原理：易证明对于每一种i(i<k)个矩形的情形，其结果一定不是最优的（可将其中某个矩形再次划分）

　　每个矩形只需记录其4至点，即可求面积。

#include<iostream>
#include<cstdio>
using namespace std;

int n,k,ans=0x7fffffff;
struct Coordinate{
    int x,y; 
}nate[102];

struct Rectangle{
    int urcorner,ulcorner,dlcorner,drcorner;
    bool flag;
}rect[12];

bool in(Rectangle a,int x,int y){
    if(x>=a.ulcorner&&x<=a.urcorner&&y>=a.dlcorner&&y<=a.drcorner) return 1;
    return 0;
}

int judge(Rectangle a,Rectangle b){
    if(in(a,b.ulcorner,b.drcorner)) return 1;
    if(in(a,b.ulcorner,b.dlcorner)) return 1;
    if(in(a,b.urcorner,b.drcorner)) return 1;
    if(in(a,b.urcorner,b.dlcorner)) return 1;
    return 0;
}

void dfs(int num){
    int area=0;
    for(int i=1; i<=k; i++) {
        if(rect[i].flag) {
            for(int j=i+1;j<=k;j++)
                if(rect[i].flag&&judge(rect[i],rect[j])) return ;
        }
        area+=(rect[i].urcorner-rect[i].ulcorner)*(rect[i].drcorner-rect[i].dlcorner);
    }
    if(area>=ans) return ;
    if(num>n) {
        ans=area;
        return ;
    }
    for(int i=1; i<=k; i++){
        Rectangle tmp=rect[i];
        if(!rect[i].flag) {
            rect[i].flag = 1;
            rect[i].ulcorner = rect[i].urcorner = nate[num].x;
            rect[i].drcorner = rect[i].dlcorner = nate[num].y;
            dfs(num+1);
            rect[i] = tmp;
            break ;
        }
        else {
            rect[i].ulcorner = min(rect[i].ulcorner,nate[num].x);
            rect[i].dlcorner = min(rect[i].dlcorner,nate[num].y);
            rect[i].urcorner = max(rect[i].urcorner,nate[num].x);
            rect[i].drcorner = max(rect[i].drcorner,nate[num].y);
            dfs(num+1);
            rect[i] = tmp;
        }
    }
}

int main() {
    cin>>n>>k;
    for(int i=1; i<=n; i++) 
        cin>>nate[i].x>>nate[i].y;
    dfs(1);
    cout<<ans<<endl;
    return 0;
}

3.洛谷 P1041 传染病控制

题目背景

近来，一种新的传染病肆虐全球。蓬莱国也发现了零星感染者，为防止该病在蓬莱国大范围流行，该国政府决定不惜一切代价控制传染病的蔓延。不幸的是，由于人们尚未完全认识这种传染病，难以准确判别病毒携带者，更没有研制出疫苗以保护易感人群。于是，蓬莱国的疾病控制中心决定采取切断传播途径的方法控制疾病传播。经过 WHO（世界卫生组织）以及全球各国科研部门的努力，这种新兴传染病的传播途径和控制方法已经研究清楚，剩下的任务就是由你协助蓬莱国疾控中心制定一个有效的控制办法。

题目描述

研究表明，这种传染病的传播具有两种很特殊的性质；

第一是它的传播途径是树型的，一个人X只可能被某个特定的人Y感染，只要Y不得病，或者是XY之间的传播途径被切断，则X就不会得病。

第二是，这种疾病的传播有周期性，在一个疾病传播周期之内，传染病将只会感染一代患者，而不会再传播给下一代。

这些性质大大减轻了蓬莱国疾病防控的压力，并且他们已经得到了国内部分易感人群的潜在传播途径图（一棵树）。但是，麻烦还没有结束。由于蓬莱国疾控中心人手不够，同时也缺乏强大的技术，以致他们在一个疾病传播周期内，只能设法切断一条传播途径，而没有被控制的传播途径就会引起更多的易感人群被感染（也就是与当前已经被感染的人有传播途径相连，且连接途径没有被切断的人群）。当不可能有健康人被感染时，疾病就中止传播。所以，蓬莱国疾控中心要制定出一个切断传播途径的顺序，以使尽量少的人被感染。

你的程序要针对给定的树，找出合适的切断顺序。

输入输出格式

输入格式：

输入格式的第一行是两个整数n（1≤n≤300）和p。接下来p行，每一行有两个整数i和j，表示节点i和j间有边相连（意即，第i人和第j人之间有传播途径相连）。其中节点1是已经被感染的患者。

输出格式：

只有一行，输出总共被感染的人数。

输入输出样例

输入样例#1：

7 6
1 2
1 3
2 4
2 5
3 6
3 7

输出样例#1：

３

(⊙v⊙)嗯~ 代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int ans,tot,n,p,edge_head[301],tree_head[301],num_edge,num_tree,maxn;
bool vis[301];
int d[301][301];

struct Edge{
    int pre,to;
}edge[602],tree[602]; 

void edge_add(int pre,int to) {
    edge[++num_edge].pre = edge_head[pre];
    edge[num_edge].to = to;
    edge_head[pre] = num_edge;
}

void tree_add(int x,int y){
    tree[++num_tree].pre = tree_head[x];
    tree[num_tree].to = y;
    tree_head[x] = num_tree;
}

void build_tree(int x) { 
    for(int i=edge_head[x];i;i=edge[i].pre) {
        if(!vis[edge[i].to]) {
            vis[edge[i].to] = true;
            tree_add(x,edge[i].to);
            build_tree(edge[i].to);
        }
    }
}

void depth(int x,int deep){ //计算深度 
    d[deep][++d[deep][0]]=x;
    if(deep>maxn) maxn=deep;
    for(int i=tree_head[x];i;i=tree[i].pre) {
        depth(tree[i].to,deep+1);
    }
}

int change(int x,bool VIS[]){
    int s=0;
    for(int i=tree_head[x];i;i=tree[i].pre) {
        if(!VIS[tree[i].to]){
            vis[tree[i].to] = true;
            VIS[tree[i].to] = true;
            s+=change(tree[i].to,VIS)+1;
        }
    }
    return s;
}

void change2(int x,bool VIS[]){
    for(int i=tree_head[x];i;i=tree[i].pre) {
        if(VIS[tree[i].to]) {
            vis[tree[i].to] = false;
            VIS[tree[i].to] = false;
            change2(tree[i].to,VIS);
        }
    }
}

void dfs(int num,int tot) {
    if(num==maxn+1){
        if(ans<tot) ans = tot;
        return ;
    }
    bool VIS[301]; 
    memset(VIS,0,sizeof(VIS));
    int sum=0;
    for(int i=1; i<=d[num][0];i++) {
        if(!vis[d[num][i]]) {
            int x=change(d[num][i],VIS)+(vis[d[num][i]]==0);
            vis[d[num][i]] = true;
            dfs(num+1,tot+x);
            vis[d[num][i]] = false;
            change2(d[num][i],VIS);
            sum++;
        }
    }
    if(sum==0) {
        if(ans<tot) ans=tot;
    }
}

int main() {
    cin>>n>>p;
    int u,v;
    for(int i=1; i<=p; i++) {
        cin>>u>>v;
        edge_add(u,v);
        edge_add(v,u);
    }
    vis[1]=true;
    build_tree(1);
    depth(1,0);
    memset(vis,0,sizeof(vis));
    dfs(1,0);
    cout<<n-ans<<endl;
    return 0;
}

自己选的路，跪着也要走完！！！