序列自动机:
- 原理:用一个数组nxt[i][j]表示字符串从i下标开始的最近的 c = j + 'a' 这个字符出现的位置
- 举个例子:
- s = "abcca" (默认下标为1-5)
- nxt[0][0] = 1,即字符串中出现的第一个字符'a'的位置为1
- nxt[1][1] = 2,即字符串距离下标1之后的字符'b'出现的第一个位置为2
- 以此类推我们可以得到 nxt[1][0] = 5,nxt[1][2] = 3 等等
序列自动机的应用:
1、快速查找一个字符串是否是另一个字符串的子序列。
2、求解k个字符串的公共子序列个数。
例题1:
月月查华华的手机
直接求出序列自动机,多次查询即可。
点击查看折叠代码块
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6+10;
int n;
char s[maxn];
char tmp[maxn];
int len;
int nxt[maxn][26];
void SeAM(){
len = strlen(s+1);
for (int i=len;i>=1;i--){
for (int j=0;j<26;j++) nxt[i-1][j] = nxt[i][j];
nxt[i-1][s[i]-'a'] = i;
}
}
int main(){
scanf("%s",s+1);
SeAM();
cin>>n;
for (int i=1;i<=n;i++){
scanf("%s",tmp+1);
int l = strlen(tmp+1);
int flag = 1;
int pos = 0;
for (int i=1;i<=l;i++){
int p = nxt[pos][tmp[i]-'a'];
if(!p){flag=0;break;}
pos = p;
}
if(flag) puts("Yes");
else puts("No");
}
return 0;
}
例题2:
P3856 [TJOI2008]公共子串
我们设 (dp[i][j][k]) 表示串a从i开始与串b从j开始与串c从k开始的公共子序列个数
则转移方程为 (dp[i][j][k] += dp[newi][newj][newk]), 当且仅当 (nxt1[i][c]) && (nxt2[j][c]) && (nxt3[k][c]) 三个值同时不为0时成立, 0<=c<=25
(newi = nxt1[i][c])
(newj = nxt2[j][c])
(newk = nxt3[k][c])
特别的,如果 i && j && k,(dp[i][j][k]+=1)
点击查看折叠代码块
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e3+10;
int n;
char s1[maxn],s2[maxn],s3[maxn];
int nxt1[maxn][26],nxt2[maxn][26],nxt3[maxn][26];
int l1,l2,l3;
void init(){
l1 = strlen(s1+1);
for (int i=l1;i>=1;i--){
for (int j=0;j<26;j++){
nxt1[i-1][j] = nxt1[i][j];
}
nxt1[i-1][s1[i]-'a'] = i;
}
l2 = strlen(s2+1);
for (int i=l2;i>=1;i--){
for (int j=0;j<26;j++){
nxt2[i-1][j] = nxt2[i][j];
}
nxt2[i-1][s2[i]-'a'] = i;
}
l3 = strlen(s3+1);
for (int i=l3;i>=1;i--){
for (int j=0;j<26;j++){
nxt3[i-1][j] = nxt3[i][j];
}
nxt3[i-1][s3[i]-'a'] = i;
}
}
ll dp[200][200][200];
ll dfs(int p1,int p2,int p3){
if(dp[p1][p2][p3]) return dp[p1][p2][p3];
for (int i=0;i<26;i++){
if(nxt1[p1][i] && nxt2[p2][i] && nxt3[p3][i]){
dp[p1][p2][p3] += dfs(nxt1[p1][i],nxt2[p2][i],nxt3[p3][i]);
}
}
if(p1 && p2 && p3) dp[p1][p2][p3]++;
return dp[p1][p2][p3];
}
int main(){
scanf("%s%s%s",s1+1,s2+1,s3+1);
init();
ll ans = dfs(0,0,0);
cout<<ans;
return 0;
}
例题3:

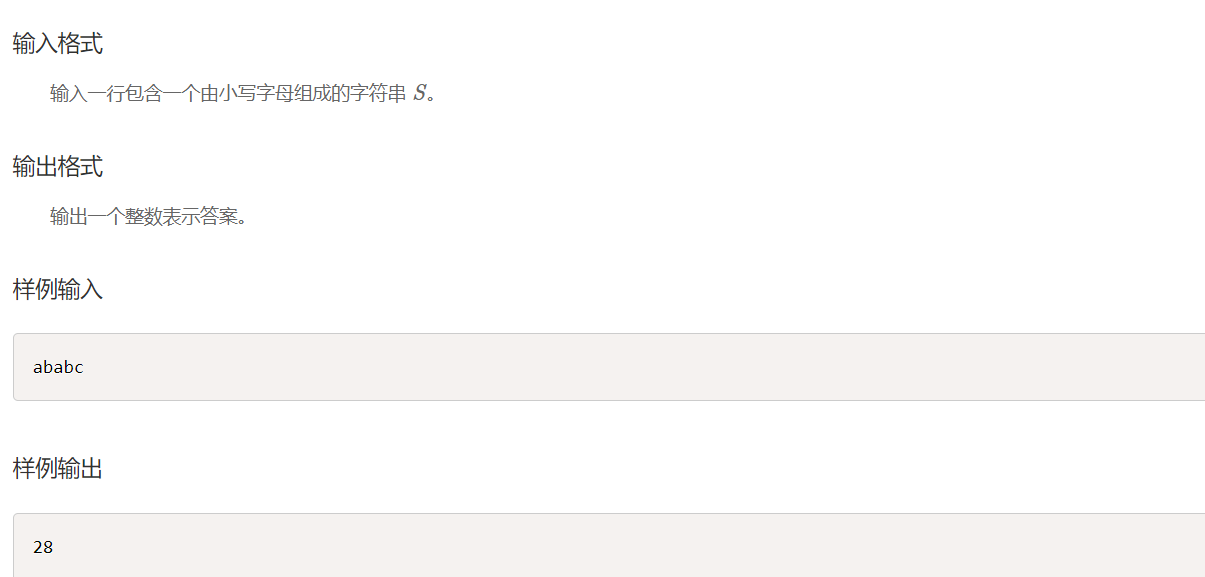
我们固定左端点l,然后枚举c = 'a'-'z'每个字符在l后出现的第一个位置为p,则以l为左端点,p到n为右端点的所有的子串都对答案有1的贡献
点击查看折叠代码块
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
int n;
char s[maxn];
int nxt[maxn][26];
void init(){
for (int i=n;i>=1;i--){
for (int j=0;j<26;j++) nxt[i-1][j] = nxt[i][j];
nxt[i-1][s[i]-'a'] = i;
}
}
int main(){
cin>>(s+1);
n = strlen(s+1);
init();
ll ans = 0;
for (int i=1;i<=n;i++){
for (int j=0;j<26;j++){
int p = nxt[i-1][j];
if(!p) continue;
ans += (n-p+1);
}
}
cout<<ans<<endl;
return 0;
}