图

1.学习总结

1.2图结构学习体会

图结构

• 邻接矩阵: 用二维矩阵储存图中边的信息.邻接矩阵简单直观,可以方便地查询任意一对顶点间的连接信息,但是对于稀疏图会浪费较大的空间.
• 邻接表: 用数组储存各顶点信息,每个数组元素有一成员用于储存顶点信息,另一成员为该顶点的边链表的头结点.邻接表方便找一个顶点的所有邻接点,对于稀疏图节约空间.容易计算顶点的出度但不好计算入度.

图遍历

• 深度优先遍历: dfs先访问起始点v0,然后以它的领接点为起始点递归访问领接点.每有一条路走到尽头,就回到上一个路口,选择另一条路再走到底,直到所有结点都已访问过.沿途标记结点已被访问.
• 广度优先遍历: bfs从第一个顶点开始访问其领接点,将这些点入栈(队).然后循环取出栈顶(队首)作上述操作,直到所有点都访问过.访问过程中标记顶点,不重复访问.

最小生成树

• Prim算法: 一开始图中只有一个点,然后不断寻找离该图最近的点并将其加入图中直到所有可连通的点都加入图中.另外也可以用Kruscal算法构建最小生成树.

最短路径

• Dijstra算法
• Floyd算法

拓扑排序

2.PTA实验作业

题目1 : 六度空间

设计思路

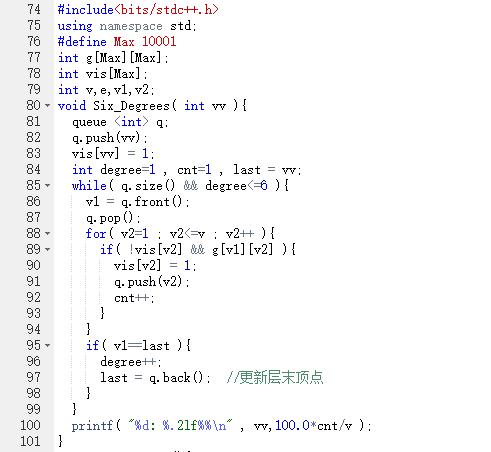
Six_Degrees(图遍历) :

定义队列 q 存放顶点, cnt 统计朋友数, last 记录该层最后一个顶点, degree 记录深度
初始化 vis 数组为 0 
起始点v0入队, vis[v0] = 1
while 队不为空 do:
    取队首 v
    for i=1 to n do:
        if  边连通且顶点 i 为访问过
            then 顶点 i 入队, vis[i]=1, cnt++
        end if
    end
    if  v 为该层最后一个结点(last)
        then  将下一层的最后一个结点(q.back)置为新的层末顶点, degree++
    end if
end

代码截图

PTA提交列表说明

题目2 : 畅通工程之最低成本建设问题

设计思路

Prim(最小生成树) :

定义变量 sum 储存总成本, dist[] 各点连接生成树的最低代价
for v2=1 to n do:
    dist[v2] = g[v0][v2];
end
dist[v0]=0
for i=1 to n-1 do:
    遍历找出进入生成树代价最小的点 v1
    if 找不到新的点
        说明图不畅通(找不齐n个点), 输出错误并结束.
    end if
    计入连接该点的花费 sum += dist[v1]
    dist[v1]=0
    遍历个点,如果通过v1进入生成代价比原来低,更新dist
end
输出总价格

代码截图

PTA提交列表说明

题目3 : 旅游规划

设计思路

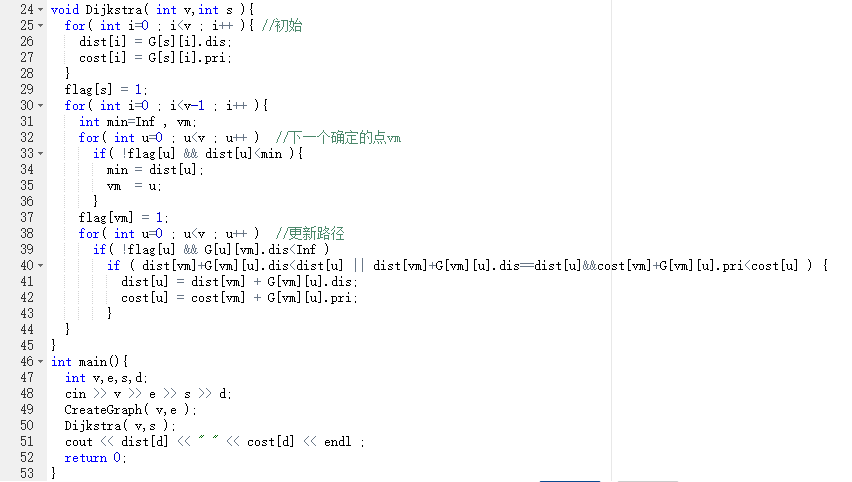
Dijstra(最短路径) :

定义dist[]数组记录各点和起始点的最短距离,path[]记录路径,cost[]记录花费,flag[]记录是否已确定路径
初始化
for i=1 to n-1 do:
    遍历找到离图最近的点 v
    将 v 加入图中 flag[v]=1
    遍历与v1连接且还没加入图的点
        if 新路线比原路线短或新路线和原路线等长但新路线比较便宜
            更新dist[],cost[]
        end if
end

代码截图

PTA提交列表说明

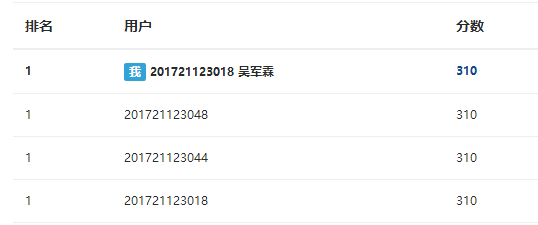
3.截图本周题目集的PTA最后排名

PTA排名

我的总分：310

4.阅读代码