一个连通图的生成树是一个极小的连通子图,它包含图中全部的顶点(n个顶点),但只有n-1条边。
最小生成树:构造连通网的最小代价(最小权值)生成树。
prim算法在严蔚敏树上有解释,但是都是数学语言,很深奥。
最小生成树MST性质:假设N=(V,{E})是一个连通网,U是顶点集V的一个非空子集。若(u,v)是一条具有最小权值(代价)的边,
其中u∈U,v∈V-U,则必存在一颗包含边(u,v)的最小生成树。
prim算法过程为:
假设N=(V,{E})是连通图,TE是N上最小生成树中边的集合。算法从U={u0}(u0∈V),TE={}开始,
重复执行下述操作:
在所有u∈U,v∈V-U的边(u,v)∈E中找一条代价最小的边(u0,v0)并入集合TE,同时v0 并入U,直至U=V为止。
此时TE中必有n-1条边,则T=(V,{TE})为N的最小生成树。
我以图为例,看看算法过程。

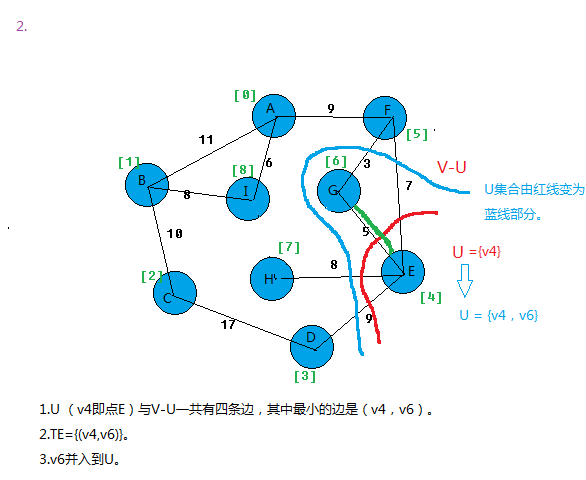
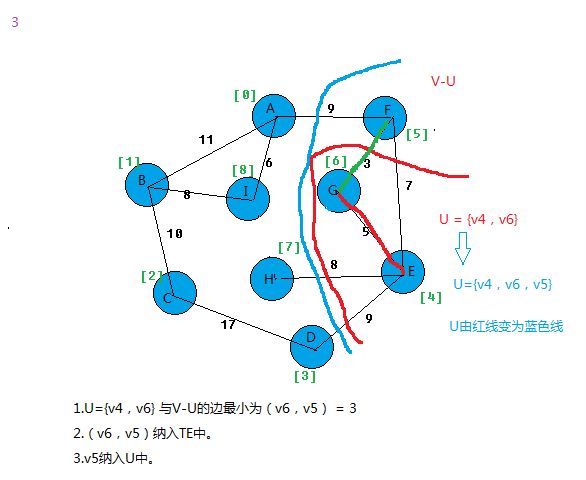
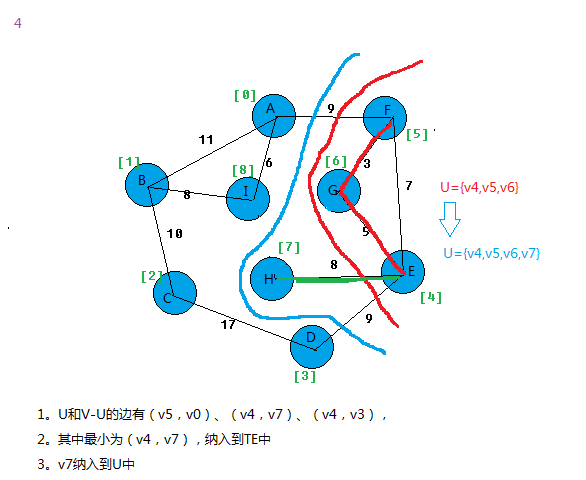
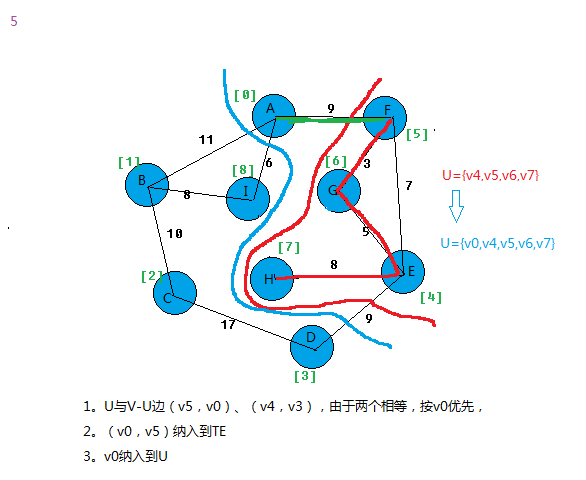
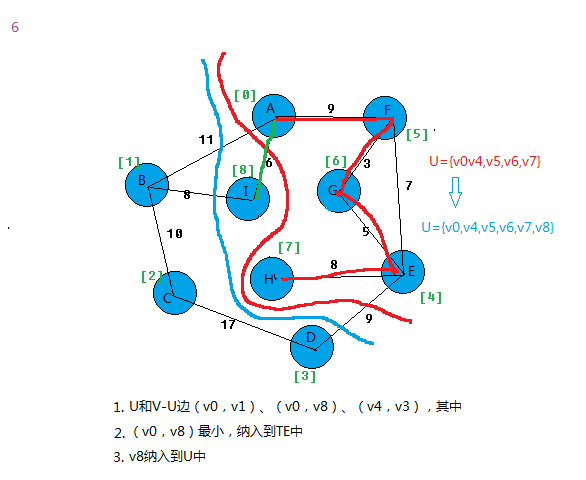
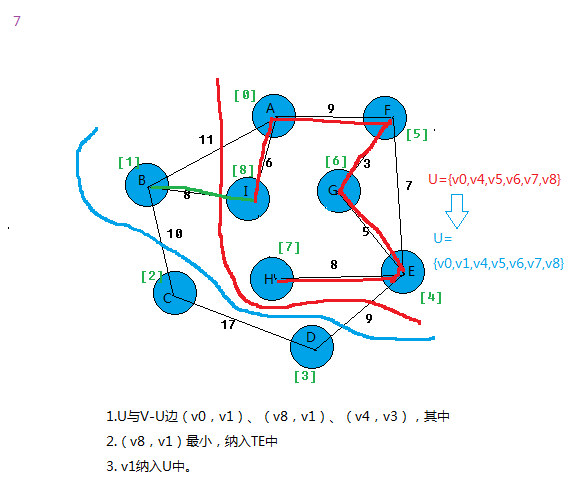
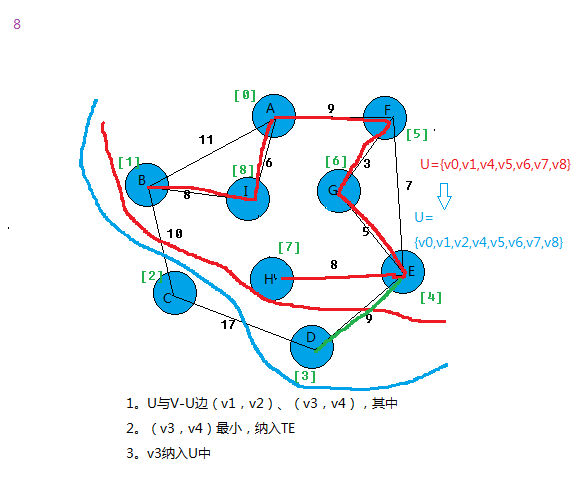
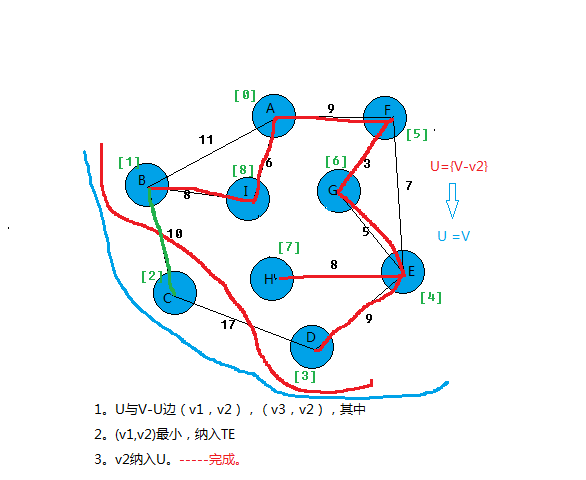
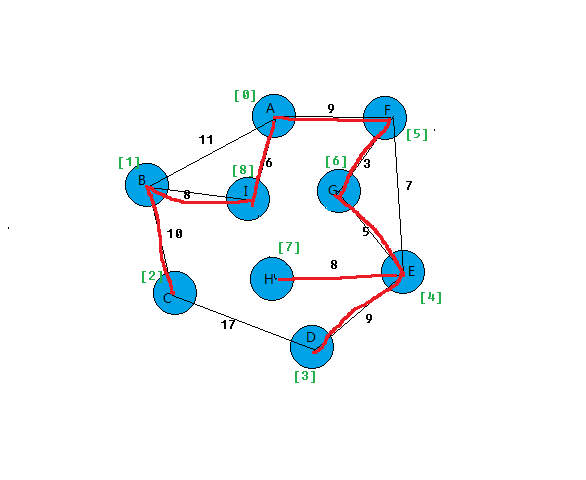
上面基本就把prim算法思想给表达出来。
代码部分:
这里我使用的是邻接矩阵来表示图,其中边的值就是权值。
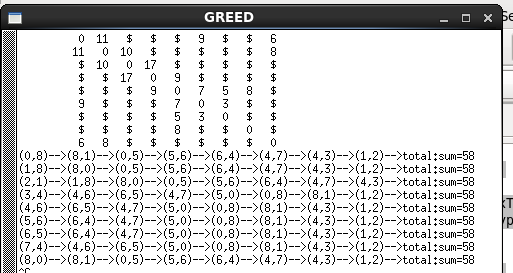
#include<stdio.h> #include<stdlib.h> typedef int bool; typedef char VertexType; typedef int EdgeType; #define false 0 #define true 1 #define MAXVEX 100 #define IFY 65535 VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'}; EdgeType g_init_edges[MAXVEX][MAXVEX] = { {0,11,IFY,IFY,IFY,9,IFY,IFY,6}, //'A' {11,0,10,IFY,IFY,IFY,IFY,IFY,8}, //'B' {IFY,10,0,17,IFY,IFY,IFY,IFY,IFY},//'C' {IFY,IFY,17,0,9,IFY,IFY,IFY,IFY},//'D' {IFY,IFY,IFY,9,0,7,5,8,IFY}, //'E' {9,IFY,IFY,IFY,7,0,3,IFY,IFY}, //'F' {IFY,IFY,IFY,IFY,5,3,0,IFY,IFY}, //'G' {IFY,IFY,IFY,IFY,8,IFY,IFY,0,IFY}, //'H' {6,8,IFY,IFY,IFY,IFY,IFY,IFY,0}, //'I' }; typedef struct { VertexType vexs[MAXVEX]; EdgeType Mat[MAXVEX][MAXVEX]; int numVexs,numEdges; }MGraph; //打印矩阵,使用二维指针 void prt_maxtix(EdgeType (*p)[MAXVEX],int vexs) { int i,j; for(i=0;i<vexs;i++) { printf(" "); for(j=0;j<vexs;j++) { if( *(*p + j) == IFY) { printf(" $ "); } else { printf(" %2d ", *(*p + j)); } } p++; printf(" "); } } //check the number of vextex int getVexNum(VertexType *vexs) { VertexType *pos = vexs; int cnt=0; while(*pos <= 'Z' && *pos >= 'A') { cnt++; pos++; } return cnt; } //检查矩阵是否对称 bool checkMat(EdgeType *p,VertexType numvex) { int i,j; for (i=0;i<numvex;i++) { for(j=i+1;j<numvex;j++) { //printf("[%d][%d] = %d ",i,j,*(p + MAXVEX*i + j)); //printf("[%d][%d] = %d ",j,i,*(p + MAXVEX*j + i)); if (*(p + MAXVEX*i + j) != *(p + MAXVEX*j +i) ) { printf("ERROR:Mat[%d][%d] or Mat[%d][%d] not equal! ",i,j,j,i); return false; } } } return true; } //用已知的一维数组和二维数组分别初始化顶点和边 void init_Grp(MGraph *g,VertexType *v,EdgeType *p) { int i,j; // init vex num (*g).numVexs = getVexNum(v); //init vexter for (i=0;i<(*g).numVexs;i++) { (*g).vexs[i]=*v; v++; } //init Mat for (i=0;i<(*g).numVexs;i++) { for (j=0;j<(*g).numVexs;j++) { (*g).Mat[i][j] = *(p + MAXVEX*i + j); } } if(checkMat(&((*g).Mat[0][0]),(*g).numVexs) == false) { printf("init error! "); exit(0); } } /*void prim(MGraph G,int num) { int sum=0; int min,i,j,k; int adjvex[MAXVEX]; int lowcost[MAXVEX]; lowcost[num] = 0; adjvex[num] = 0; for (i = 0; i < G.numVexs;i++ ) { if (num == i) { continue; } lowcost[i]=G.Mat[num][i]; //存放起始顶点到各个顶点的权值。 adjvex[i] = num; } for (i=0;i<G.numVexs;i++) { //1.找权最短路径 //2.把权最短路径的顶点纳入已找到的顶点集合中,重新查看新集合中最短路径 if(num == i) { continue; } min = IFY; j=0;k=0; while (j<G.numVexs) { if (lowcost[j] != 0 && lowcost[j] < min) { min = lowcost[j]; k = j; } j++; } printf(" (%d,%d) --> ",adjvex[k],k); sum += G.Mat[adjvex[k]][k]; lowcost[k]=0; for (j=0;j<G.numVexs;j++) { if (lowcost[j] != 0 && G.Mat[k][j] < lowcost[j]) { lowcost[j] = G.Mat[k][j]; adjvex[j]=k; } } } printf("total:sum=%d ",sum); }*/ void Prim(MGraph G,int num) { int sum,i,j,min,k; int adjvex[MAXVEX]; int lowcost[MAXVEX]; sum=0; adjvex[num]=0; lowcost[num]=0; for(i=0;i<G.numVexs;i++) { if(i==num) continue; adjvex[i]=num; lowcost[i]=G.Mat[num][i]; } for(i=0;i<G.numVexs;i++) { if(i==num) continue; min=IFY; k=0; //求出代价最小的点 for(j=0;j<G.numVexs;j++) { if(lowcost[j]!=0&&lowcost[j]<min) { min=lowcost[j]; k=j; } } printf("(%d,%d)-->",adjvex[k],k); sum+=G.Mat[adjvex[k]][k]; lowcost[k]=0; for(j=0;j<G.numVexs;j++) { if(lowcost[j]!=0&&G.Mat[k][j]<lowcost[j]) { lowcost[j]=G.Mat[k][j]; adjvex[j]=k; } } } printf("total:sum=%d ",sum); } int main(int argc, char* argv[]) { MGraph grp; //init init_Grp(&grp,g_init_vexs,&g_init_edges[0][0]); //print Matix prt_maxtix(grp.Mat,grp.numVexs); //prim(grp,4); int i; for (i=0;i<grp.numVexs;i++) { Prim(grp,i); } //prim(grp,3); getchar(); return 0; }
运行结果如下: