拓扑排序介绍
拓扑排序(Topological Order)是指,将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列。
这样说,可能理解起来比较抽象。下面通过简单的例子进行说明!
例如,一个项目包括A、B、C、D四个子部分来完成,并且A依赖于B和D,C依赖于D。现在要制定一个计划,写出A、B、C、D的执行顺序。这时,就可以利用到拓扑排序,它就是用来确定事物发生的顺序的。
在拓扑排序中,如果存在一条从顶点A到顶点B的路径,那么在排序结果中B出现在A的后面。
拓扑排序的算法图解
拓扑排序算法的基本步骤:
1. 构造一个队列Q(queue) 和 拓扑排序的结果队列T(topological);
2. 把所有没有依赖顶点的节点放入Q;
3. 当Q还有顶点的时候,执行下面步骤:
3.1 从Q中取出一个顶点n(将n从Q中删掉),并放入T(将n加入到结果集中);
3.2 对n每一个邻接点m(n是起点,m是终点);
3.2.1 去掉边<n,m>;
3.2.2 如果m没有依赖顶点,则把m放入Q;
注:顶点A没有依赖顶点,是指不存在以A为终点的边。
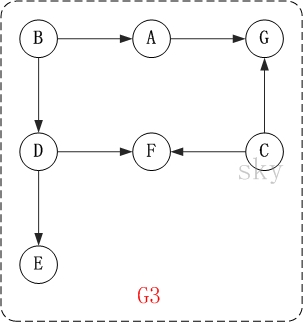
以上图为例,来对拓扑排序进行演示。
第1步:将B和C加入到排序结果中。
顶点B和顶点C都是没有依赖顶点,因此将C和C加入到结果集T中。假设ABCDEFG按顺序存储,因此先访问B,再访问C。访问B之后,去掉边<B,A>和<B,D>,并将A和D加入到队列Q中。同样的,去掉边<C,F>和<C,G>,并将F和G加入到Q中。
(01) 将B加入到排序结果中,然后去掉边<B,A>和<B,D>;此时,由于A和D没有依赖顶点,因此并将A和D加入到队列Q中。
(02) 将C加入到排序结果中,然后去掉边<C,F>和<C,G>;此时,由于F有依赖顶点D,G有依赖顶点A,因此不对F和G进行处理。
第2步:将A,D依次加入到排序结果中。
第1步访问之后,A,D都是没有依赖顶点的,根据存储顺序,先访问A,然后访问D。访问之后,删除顶点A和顶点D的出边。
第3步:将E,F,G依次加入到排序结果中。
因此访问顺序是:B -> C -> A -> D -> E -> F -> G
拓扑排序的代码说明
拓扑排序是对有向无向图的排序。下面以邻接表实现的有向图来对拓扑排序进行说明。
1. 基本定义
// 邻接表中表对应的链表的顶点 typedef struct _ENode { int ivex; // 该边所指向的顶点的位置 struct _ENode *next_edge; // 指向下一条弧的指针 }ENode, *PENode; // 邻接表中表的顶点 typedef struct _VNode { char data; // 顶点信息 ENode *first_edge; // 指向第一条依附该顶点的弧 }VNode; // 邻接表 typedef struct _LGraph { int vexnum; // 图的顶点的数目 int edgnum; // 图的边的数目 VNode vexs[MAX]; }LGraph;
(01) LGraph是邻接表对应的结构体。 vexnum是顶点数,edgnum是边数;vexs则是保存顶点信息的一维数组。
(02) VNode是邻接表顶点对应的结构体。 data是顶点所包含的数据,而firstedge是该顶点所包含链表的表头指针。
(03) ENode是邻接表顶点所包含的链表的节点对应的结构体。 ivex是该节点所对应的顶点在vexs中的索引,而nextedge是指向下一个节点的。
2. 拓扑排序
/* * 拓扑排序 * * 参数说明: * G -- 邻接表表示的有向图 * 返回值: * -1 -- 失败(由于内存不足等原因导致) * 0 -- 成功排序,并输入结果 * 1 -- 失败(该有向图是有环的) */ int topological_sort(LGraph G) { int i,j; int index = 0; int head = 0; // 辅助队列的头 int rear = 0; // 辅助队列的尾 int *queue; // 辅组队列 int *ins; // 入度数组 char *tops; // 拓扑排序结果数组,记录每个节点的排序后的序号。 int num = G.vexnum; ENode *node; ins = (int *)malloc(num*sizeof(int)); // 入度数组 tops = (char *)malloc(num*sizeof(char));// 拓扑排序结果数组 queue = (int *)malloc(num*sizeof(int)); // 辅助队列 assert(ins!=NULL && tops!=NULL && queue!=NULL); memset(ins, 0, num*sizeof(int)); memset(tops, 0, num*sizeof(char)); memset(queue, 0, num*sizeof(int)); // 统计每个顶点的入度数 for(i = 0; i < num; i++) { node = G.vexs[i].first_edge; while (node != NULL) { ins[node->ivex]++; node = node->next_edge; } } // 将所有入度为0的顶点入队列 for(i = 0; i < num; i ++) if(ins[i] == 0) queue[rear++] = i; // 入队列 while (head != rear) // 队列非空 { j = queue[head++]; // 出队列。j是顶点的序号 tops[index++] = G.vexs[j].data; // 将该顶点添加到tops中,tops是排序结果 node = G.vexs[j].first_edge; // 获取以该顶点为起点的出边队列 // 将与"node"关联的节点的入度减1; // 若减1之后,该节点的入度为0;则将该节点添加到队列中。 while(node != NULL) { // 将节点(序号为node->ivex)的入度减1。 ins[node->ivex]--; // 若节点的入度为0,则将其"入队列" if( ins[node->ivex] == 0) queue[rear++] = node->ivex; // 入队列 node = node->next_edge; } } if(index != G.vexnum) { printf("Graph has a cycle "); free(queue); free(ins); free(tops); return 1; } // 打印拓扑排序结果 printf("== TopSort: "); for(i = 0; i < num; i ++) printf("%c ", tops[i]); printf(" "); free(queue); free(ins); free(tops); return 0; }
说明:
(01) queue的作用就是用来存储没有依赖顶点的顶点。它与前面所说的Q相对应。
(02) tops的作用就是用来存储排序结果。它与前面所说的T相对应。
拓扑排序的完整源码和测试程序
c实现代码:
#include<stdlib.h> #include<stdio.h> #include<string.h> #include<malloc.h> #define MAX 100 typedef struct ENode { int ivex; struct ENode *next_edge; }ENode; typedef struct VNode { char data; struct ENode *first_edge; }VNode; typedef struct LGraph { int vexnum; int edgnum; VNode vexs[MAX]; }LGraph; int get_position(LGraph g,char ch) { int i; for(i=0;i<g.vexnum;i++) if(ch==g.vexs[i].data) return i; return -1; } LGraph* create_graph() { char vexs[]= {'A','B','C','D','E','F','G'}; char edges[][2]= {{'A','C'},{'B','A'},{'B','D'},{'C','F'},{'C','G'},{'D','E'},{'D','F'}}; int vlen=sizeof(vexs)/sizeof(vexs[0]); int elen=sizeof(edges)/sizeof(edges[0]); int i,p1,p2; ENode *node2; LGraph *pG; if((pG=(LGraph*)malloc(sizeof(LGraph)))==NULL) return NULL; memset(pG,0,sizeof(pG)); pG->edgnum=elen; pG->vexnum=vlen; for(i=0;i<pG->vexnum;i++) { pG->vexs[i].data=vexs[i]; pG->vexs[i].first_edge=NULL; } for(i=0;i<pG->edgnum;i++) { p1=get_position(*pG,edges[i][0]); p2=get_position(*pG,edges[i][1]); node2=(ENode*)malloc(sizeof(ENode)); node2->ivex=p2; node2->next_edge=NULL; if(pG->vexs[p1].first_edge==NULL) pG->vexs[p1].first_edge=node2; else { ENode *tmp=pG->vexs[p1].first_edge; while(tmp->next_edge) { tmp=tmp->next_edge; } tmp->next_edge=node2; } } return pG; } void print_graph(LGraph G) { int i; printf("List Graph: "); ENode *node=NULL; for(i=0;i<G.vexnum;i++) { printf("%d(%c): ", i, G.vexs[i].data); node=G.vexs[i].first_edge; while(node) { printf("%d(%c) ", node->ivex, G.vexs[node->ivex].data); node=node->next_edge; } printf(" "); } } int topological_sort(LGraph G) { int i,j; int index = 0; int head = 0; // 辅助队列的头 int rear = 0; // 辅助队列的尾 int *queue; // 辅组队列 int *ins; // 入度数组 char *tops; // 拓扑排序结果数组,记录每个节点的排序后的序号。 int num = G.vexnum; ENode *node; ins = (int *)malloc(num*sizeof(int)); // 入度数组 tops = (char *)malloc(num*sizeof(char));// 拓扑排序结果数组 queue = (int *)malloc(num*sizeof(int)); // 辅助队列 memset(ins, 0, num*sizeof(int)); memset(tops, 0, num*sizeof(char)); memset(queue, 0, num*sizeof(int)); // 统计每个顶点的入度数 for(i = 0; i < num; i++) { node = G.vexs[i].first_edge; while (node != NULL) { ins[node->ivex]++; node = node->next_edge; } } // 将所有入度为0的顶点入队列 for(i = 0; i < num; i ++) if(ins[i] == 0) queue[rear++] = i; // 入队列 while (head != rear) // 队列非空 { j = queue[head++]; // 出队列。j是顶点的序号 tops[index++] = G.vexs[j].data; // 将该顶点添加到tops中,tops是排序结果 node = G.vexs[j].first_edge; // 获取以该顶点为起点的出边队列 // 将与"node"关联的节点的入度减1; // 若减1之后,该节点的入度为0;则将该节点添加到队列中。 while(node != NULL) { // 将节点(序号为node->ivex)的入度减1。 ins[node->ivex]--; // 若节点的入度为0,则将其"入队列" if( ins[node->ivex] == 0) queue[rear++] = node->ivex; // 入队列 node = node->next_edge; } } if(index != G.vexnum) { printf("Graph has a cycle "); free(queue); free(ins); free(tops); return 1; } // 打印拓扑排序结果 printf("== TopSort: "); for(i = 0; i < num; i ++) printf("%c ", tops[i]); printf(" "); free(queue); free(ins); free(tops); return 0; } int topologicalOrder(LGraph G) { int i,j; int index=0; int front=0; int rear=0; int *queue; int *ins; char *tops; int num=G.vexnum; ENode *node; ins=(int *)malloc(num*sizeof(int)); tops=(char *)malloc(num*sizeof(char)); queue=(int *)malloc(num*sizeof(int)); memset(ins,0,num*sizeof(ins)); memset(tops,0,num*sizeof(tops)); memset(queue,0,num*sizeof(queue)); for(i=0;i<num;i++) { node=G.vexs[i].first_edge; //统计每个结点的入度数 while(node) { ins[node->ivex]++; node=node->next_edge; } } //将入度数为0的结点加入到queue中 for(i=0;i<num;i++) { if(ins[i]==0) queue[rear++]=i; } while(front!=rear) { j=queue[front++]; tops[index++]=G.vexs[j].data; node=G.vexs[j].first_edge; while(node) { ins[node->ivex]--; if(ins[node->ivex]==0) queue[rear++]=node->ivex; node=node->next_edge; } } if(index!=G.vexnum) { printf("Graph has a cycle "); free(queue); free(ins); free(tops); return 1; } // 打印拓扑排序结果 printf("TopSort: "); for(i = 0; i < num; i ++) printf("%c ", tops[i]); printf(" "); free(queue); free(ins); free(tops); return 0; } int main() { LGraph *pG; pG=create_graph(); print_graph(*pG); topologicalOrder(*pG); }
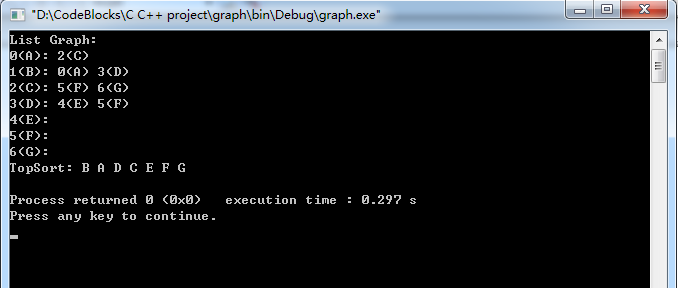
运行结果: