博客也开了挺长时间了,一直都没有来写博客,主要原因是自己懒~~~此篇博客算是给2017年一个好的开始,同时也给2016年画上一个句点,不留遗憾。
那就让我们正式进入今天的主题:贝塞尔曲线。
首先,让我们来了解下什么是贝塞尔曲线。
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。贝塞尔曲线于1962,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发,以稳定数值的方法求出贝兹曲线。

了解了什么是贝塞尔曲线,接下来我们来看看贝塞尔曲线的分类。再讲分类之前,首先要提到的两个概念:数据点和控制点。
数据点:曲线的起始点和终点。
控制点:顾名思义,就是控制曲线的弯曲程度的点。
曲线主要有以下分类:
一阶曲线:
公式: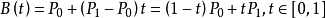
动态图: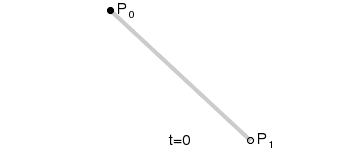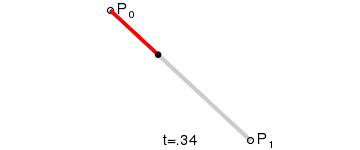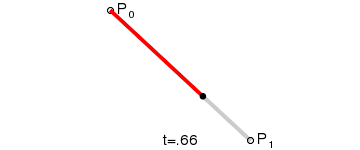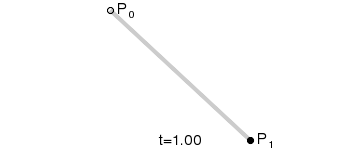
原理:从P0(起始点)到P1(终点)之间连续的点组成的一条直线。一阶曲线是没有控制点的。
二阶曲线:
公式: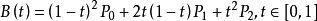
静态图: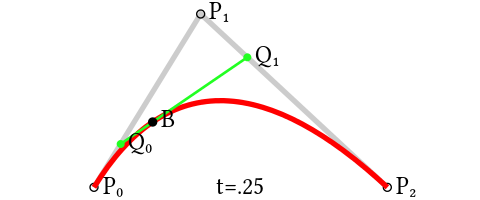
动态图: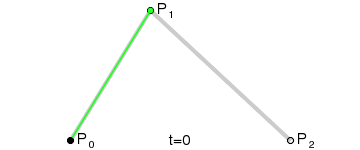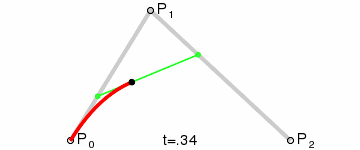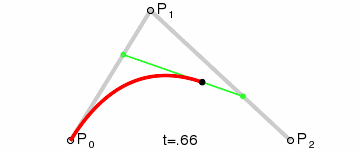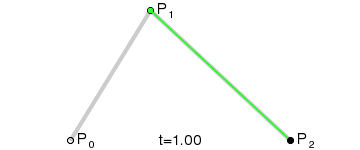
原理:点Q0(t)的变化从P0到P1,描述一个线性Bézier曲线。
点Q1(t)的变化从P1到P2,描述了一个线性Bézier曲线。
B点(t)的变化从Q0(t)到Q1(t),描述了一个二次Bézier曲线。
P0为起始点,P2为终点,P1为控制点。
三阶曲线:
公式: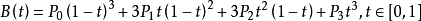
静态图: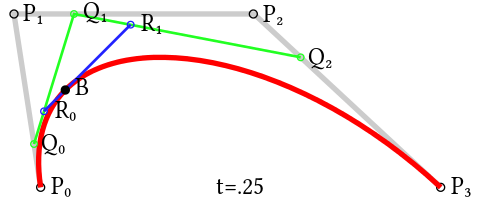
动态图:
原理:其原理和二阶曲线的原理类似,主要是多了个控制点。
除了以上三种贝塞尔曲线的分类,当然还有四阶曲线、五阶曲线...........
说了这么多了,那我们到底该如何使用贝塞尔曲线呢,有没有方法提供给我们呢?
当然有提供给我们的,在我们自定义View的时候,会用到一个叫Path的类,在这个类中,存在两个方法:quadTo(绘制二阶曲线), cubicTo(绘制三阶曲线)。这两个方法我会简单的用两段代码来说明下。这里我会贴出主要的代码:
二阶曲线主要代码块:
@Override
protected void onDraw(Canvas canvas) {
//画直线
mPaint.setColor(Color.BLACK);
mPaint.setStrokeWidth(4);
canvas.drawLine(firstPoint.x,firstPoint.y,midPoint.x,midPoint.y,mPaint);
canvas.drawLine(lastPoint.x,lastPoint.y,midPoint.x,midPoint.y,mPaint);
//画点
mPaint.setStrokeWidth(20);
canvas.drawPoint(firstPoint.x,firstPoint.y,mPaint);
canvas.drawPoint(lastPoint.x,lastPoint.y,mPaint);
canvas.drawPoint(midPoint.x,midPoint.y,mPaint);
//画二阶曲线
mPaint.setColor(Color.BLUE);
mPaint.setStrokeWidth(8);
Path path = new Path();
path.moveTo(firstPoint.x,firstPoint.y);
path.quadTo(midPoint.x,midPoint.y,lastPoint.x,lastPoint.y);
canvas.drawPath(path,mPaint);
}
效果图: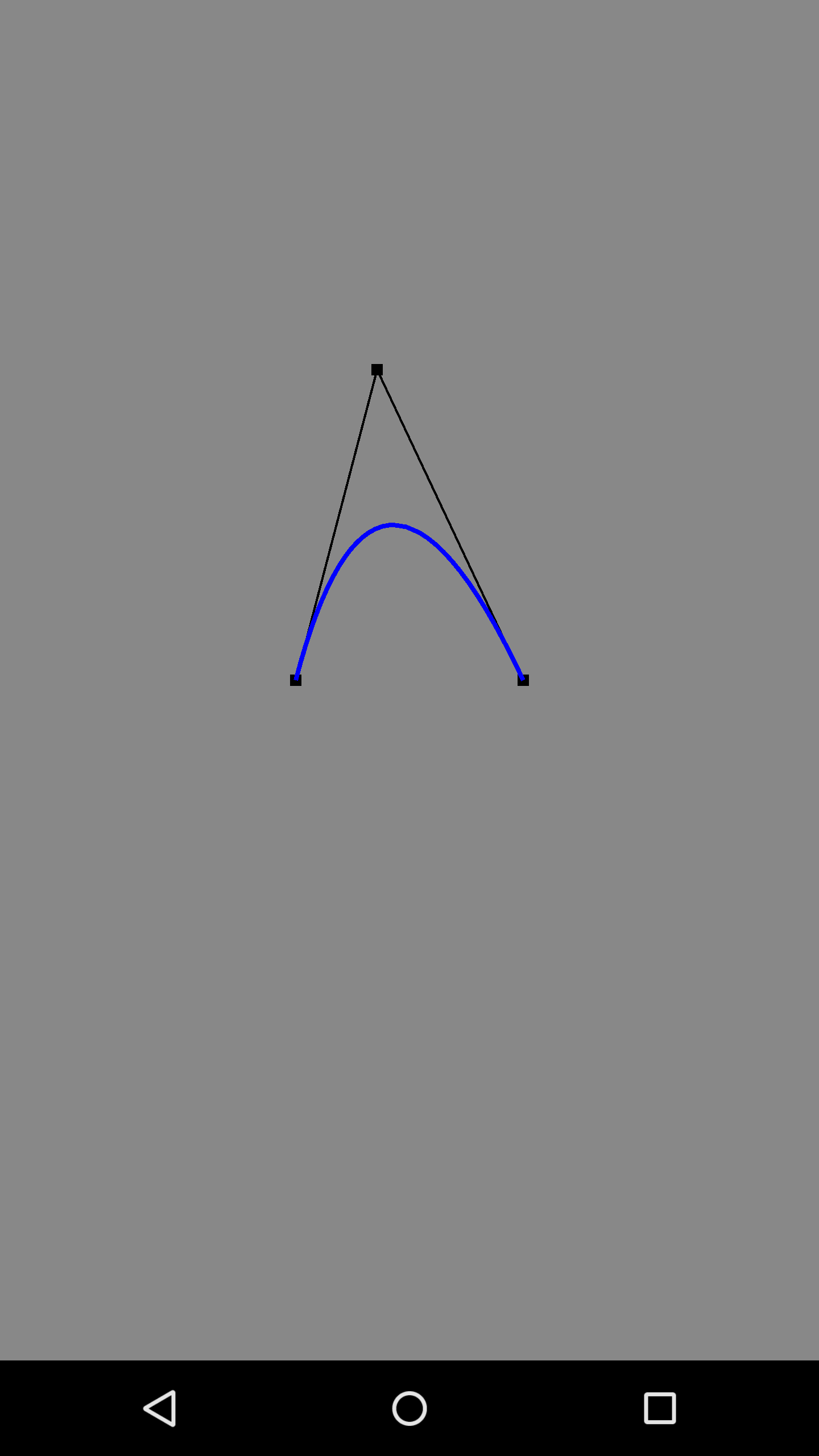 (ps:不会在手机上弄动态图
(ps:不会在手机上弄动态图![]() )
)
三阶曲线主要代码块:
@Override
protected void onDraw(Canvas canvas) {
mPaint.setColor(Color.BLACK);
//画直线
mPaint.setStrokeWidth(4);
canvas.drawLine(firstPoint.x,firstPoint.y,control1.x,control1.y,mPaint);
canvas.drawLine(midPoint1.x,midPoint1.y,midPoint2.x,midPoint2.y,mPaint);
canvas.drawLine(midPoint2.x,midPoint2.y,lastPoint.x,lastPoint.y,mPaint);
//画点
mPaint.setStrokeWidth(20);
canvas.drawPoint(firstPoint.x,firstPoint.y,mPaint);
canvas.drawPoint(lastPoint.x,lastPoint.y,mPaint);
canvas.drawPoint(midPoint1.x,midPoint1.y,mPaint);
canvas.drawPoint(midPoint2.x,midPoint2.y,mPaint);
//画三阶曲线
mPaint.setColor(Color.BLUE);
mPaint.setStrokeWidth(8);
Path path = new Path();
path.moveTo(firstPoint.x,firstPoint.y);
path.cubicTo(midPoint1.x,midPoint1.y,midPoint2.x,midPoint2.y,
lastPoint.x,lastPoint.y);
canvas.drawPath(path,mPaint);
}
效果图: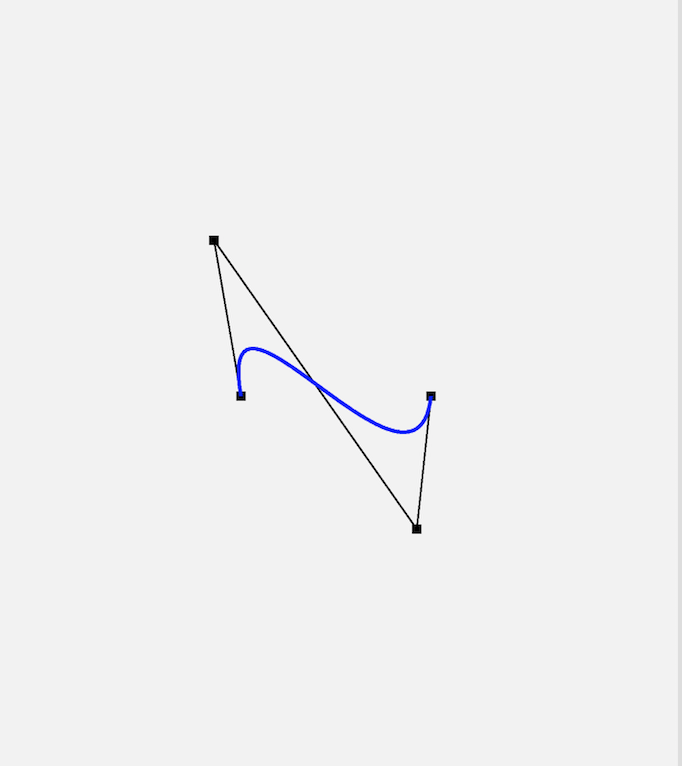 (ps:还是不会在手机上弄动态图
(ps:还是不会在手机上弄动态图![]() )
)
好了,至此,贝塞尔曲线的浅析已经讲完了,如还想更多去了解贝塞尔曲线,可以看看这个网站:
https://en.wikipedia.org/wiki/B%C3%A9zier_curve
由于第一次写博客,有些地方表达的不是很好,还请谅解。如有好的建议和不足之处还望指出,一定虚心更改。