LeetCode 28. Implement strStr()

退役选手开始刷LeetCode重温算法，没想到KMP已经忘得一干二净了，整理一下思路

KMP算法就是对于下面用来匹配的串，因为我们已经知道比较到 P[j] 的时候， S[i - 1, i - j] 的部分和 P[j - 1, 0 ] 的部分是匹配的

那么我们如果知道P[j - 1] 的最长相等前缀(p[j - 1, j - k] = p[k - 1, 0])，那么不需要挪动 i, 需要把 j  移动到 k 开始比较就可以了。 

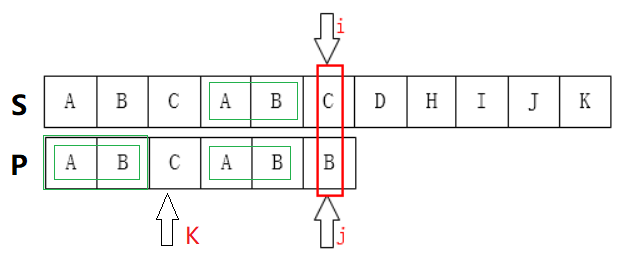
所以问题就在于我们要初始化一个数组 next 用来计算 P 每个位置对应的最长前缀

定义 next[j] = k 表示 P[j - 1, j - k] = P[k - 1, 0]

next 的求解代码如下

vector<int> getNext(string s) {
    int j = 0;
    int k = -1;
    int m = s.length();
    vector<int> next(m);
    next[0] = -1;
    while(j < m - 1) {
        if(k == -1 || s[j] == s[k])
            next[++j] = ++k;
        else    
            k = next[k];
    }
    return next;
}

例如上图的 P 计算得到的 next

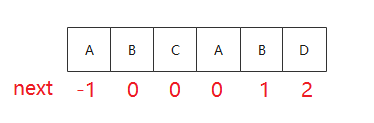
其中 next[0] = -1 是因为 j = 0 时无法再左移了， 因此需要移动 i 了

 当 P[j] == P[k] 时很好解决 因为 P[j - 1, j - k - 1] = P[k - 1, 0], 所以 P[j, j - k - 1] = P[k , 0]

 只需 next[j + 1] = k + 1 即可 如下图例子

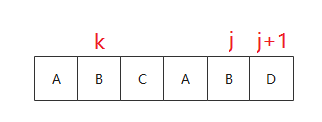
当 P[j] != P[k]  时， 意味着当前的前缀不能再延长了， 为了获取新的最长前缀，我们需要查看下一个可能的最长前缀

所以这就是  k = next[k] 的原因

如下图，我们知道 P[j - 1, j - k] = p[k - 1, 0], 而 p[k - 1, k - next[k]] = p[next[k] - 1, 0] 所以这三部分是相同的， 因此next[k] 前面的部分就是可能的最长前缀。

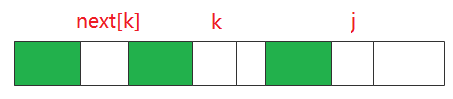
 可以用下面的例子推导一下

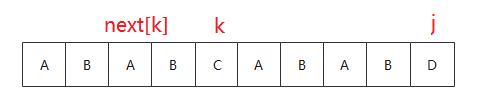
OK, KMP的部分就结束了，下面上代码

class Solution {
public:
    
    vector<int> getNext(string s) {
        int j = 0;
        int k = -1;
        int m = s.length();
        vector<int> next(m);
        next[0] = -1;
        while(j < m - 1) {
            if(k == -1 || s[j] == s[k])
                next[++j] = ++k;
            else    
                k = next[k];
        }
        return next;
    }

    int strStr(string haystack, string needle) {
        int n = haystack.length(), m = needle.length();
        if(m == 0)
            return 0;
        vector<int> next = getNext(needle);
        int i = 0, j = 0;
        while(i < n && j < m) {
            if(j == -1 || haystack[i] == needle[j]) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
        if(j == m)
            return i - j;
        return -1;
    }
};