Is Derek lying?
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1003 Accepted Submission(s): 548
For each test case,there will be three lines.
The first line consists of three integers N
The second line consists of N
The third line consists of N
Data Range:1≤N≤80000
Please print “Lying

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clrmax(x) memset(x,0,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 using namespace std; 7 char s1[80010],s2[80010]; 8 int min(int a,int b) 9 { 10 return a<b?a:b; 11 } 12 int main() 13 { 14 int T,same,dif,x,y,n; 15 scanf("%d",&T); 16 for(int kase=1;kase<=T;kase++) 17 { 18 scanf("%d%d%d",&n,&x,&y); 19 cin>>s1; 20 cin>>s2; 21 same=0; 22 for(int i=0;i<n;i++) 23 if(s1[i]==s2[i]) 24 same++; 25 dif=n-same; 26 if(dif>=abs(x-y) && (dif-abs(x-y))/2+same>=min(x,y)) 27 printf("Not lying "); 28 else 29 printf("Lying "); 30 } 31 return 0; 32 }
Maximum Sequence
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1405 Accepted Submission(s): 649
Given two integer sequences {ai} and {bi} with the same length n, you are to find the next n numbers of {ai}: a
Now Steph finds it too hard to solve the problem, please help him.
For each test case, the first line consists of one integer n. The next line consists of n integers representing {ai}. And the third line consists of n integers representing {bi}.
1≤n≤250000, n≤a_i≤1500000, 1≤b_i≤n.
也是签到题。很容易想到的贪心:每次我们取当前数列中能取的数减去其位置的结果,最大的一个放到数列后面作为该位置的值。因此我们维护一个大根堆,以数-位置作为关键字,存放可取的数以及该数所在的位置。维护一个二叉搜索树,动态存取我们可以取的bi。大根堆用stl的优先队列,二叉搜索树用stl的multiset替代。那么每次加入ai时我们检查堆首的位置在multiset中有无小于他的数,有就贪心地取最近的一个作为该位置使用的bj并从multiset中去除该bi。并将该数作为该位置的值,将数-其位置 以及他的位置入堆;若没有则pop堆首直到有这样的数出现。

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clrmax(x) memset(x,0,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 using namespace std; 7 struct node 8 { 9 int pos,val; 10 bool operator < (const node &b) const 11 { 12 return val<b.val; 13 } 14 }u,v; 15 priority_queue<node> sta; 16 int n,m,t,pos,p; 17 int b[300010]; 18 multiset<int>::iterator it; 19 multiset<int> posi; 20 LL ans; 21 int main() 22 { 23 while(scanf("%d",&n)!=EOF) 24 { 25 while(!sta.empty()) 26 sta.pop(); 27 posi.erase(posi.begin(),posi.end()); 28 for(int i=1;i<=n;i++) 29 { 30 scanf("%d",&t); 31 sta.push((node){i,t-i}); 32 } 33 for(int i=1;i<=n;i++) 34 { 35 scanf("%d",&t); 36 posi.insert(t); 37 } 38 ans=0; 39 for(int i=1;i<=n;i++) 40 { 41 while((it=posi.upper_bound(sta.top().pos))==posi.begin()) 42 sta.pop(); 43 it--; 44 ans=(ans+(LL)sta.top().val)%mod; 45 pos=i+n; 46 t=sta.top().val-pos; 47 sta.push((node){pos,t}); 48 posi.erase(it); 49 } 50 printf("%lld ",ans); 51 52 } 53 return 0; 54 }
Puzzle
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 271 Accepted Submission(s): 147
1.Sorting all the remaining jigsaws on the table in ascending order.
2.Picking out the 1st ,the P+1 th ,the 2*P+1 th,......the n*P+1 th jigsaws and put them back to the blank area in the board one by one from the top row to the bottom row,from the left column to the right column.
3.if there are jigsaws remained on the table,back to step 1.
After he arranging the board,it’s obvious that there’s only one blank area located at the bottom-right corner.
Your task is to make the numbers on jigsaws sorted with every row and every column in ascending order(From left to right,top to bottom),and the blank area should be located at the bottom-right corner in the end.Each step you can move the blank area’s neighboring jigsaws(which share a common side with the blank area) towards the blank area.It’s really a difficult question,so you need to write a program to judge whether it is possible to complete the task.

Following T lines,each line contains three integers N,M,P(2<=N,M<=1000;1<=P<=N*M-2).

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 using namespace std; 4 int main() 5 { 6 int T; 7 int n,m,p,q,t,ans,tot; 8 scanf("%d",&T); 9 while(T--) 10 { 11 ans=0; 12 scanf("%d%d%d",&n,&m,&p); 13 tot=n*m-1; 14 while(tot>p) 15 { 16 t=(tot-1)/p+1; 17 ans+=(p-1)*t*(t-1)/2; 18 tot-=t; 19 } 20 if(ans%2) 21 printf("NO "); 22 else 23 printf("YES "); 24 } 25 return 0; 26 }
Sdjpx Is Happy
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 326 Accepted Submission(s): 124
1.He can divides soldiers into K disjoint non-empty subarrays.
2.He can sort a subarray many times untill a subarray is sorted in increasing order.
3.He can choose just two subarrays and change thier positions between themselves.
Consider A = [1 5 4 3 2] and P = 2. A possible soldiers into K = 4 disjoint subarrays is:A1 = [1],A2 = [5],A3 = [4],A4 = [3 2],After Sorting Each Subarray:A1 = [1],A2 = [5],A3 = [4],A4 = [2 3],After swapping A4 and A2:A1 = [1],A2 = [2 3],A3 = [4],A4 = [5].
But he wants to know for a fixed permutation ,what is the the maximum number of K?
Notice: every soldier has a distinct number from 1~n.There are no more than 10 cases in the input.
For every case:
Next line is n.
Next line is the number for the n soildiers.
Every case a line.

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clrmax(x) memset(x,0x3f3f3f3f,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 #define N 3010 7 using namespace std; 8 int f[N][N],minx[N][N],maxx[N][N],last[N],num[N]; 9 int n,m,k; 10 inline int max(int a,int b) 11 { 12 return a>b?a:b; 13 } 14 inline int min(int a,int b) 15 { 16 return a<b?a:b; 17 } 18 void predeal(int n) 19 { 20 for(int i=1;i<=n;i++) 21 { 22 last[i]=i; 23 f[i][i]=1; 24 minx[i][i]=maxx[i][i]=num[i]; 25 for(int j=i+1;j<=n;j++) 26 { 27 minx[i][j]=min(minx[i][j-1],num[j]); 28 maxx[i][j]=max(maxx[i][j-1],num[j]); 29 } 30 } 31 int j; 32 for(int l=1;l<n;l++) 33 { 34 for(int i=1;i<=n-l;i++) 35 { 36 j=i+l; 37 if(maxx[i][j]-minx[i][j]!=j-i) 38 f[i][j]=0; 39 else 40 { 41 if(minx[i][j]<minx[i][last[i]]) 42 f[i][j]=1; 43 else 44 f[i][j]=f[i][last[i]]+f[last[i]+1][j]; 45 last[i]=j; 46 } 47 // cout<<i<<" "<<j<<":"<<f[i][j]<<endl; 48 } 49 } 50 return ; 51 } 52 int main() 53 { 54 int T,p,ans; 55 scanf("%d",&T); 56 while(T--) 57 { 58 scanf("%d",&n); 59 for(int i=1;i<=n;i++) 60 scanf("%d",&num[i]); 61 predeal(n);//处理n^2确定i~j间不用交换情况下最多分几组 62 //n^2暴力,确定要交换的靠前的区间后,就能确定靠后区间的右端点,判断是否合法,合法则枚举靠后区间的左端点看是否能合法与靠前区间交换。合法则计算其分组数。在这些分组中和不交换情况下取最大值即为答案。 63 ans=0; 64 for(int i=1;i<=n;i++) 65 for(int j=i;j<=n;j++) 66 if(f[i][j] && (i==1||(f[1][i-1] && minx[1][j-1]==1))) 67 { 68 p=maxx[i][j]; 69 if(p==n || (f[p+1][n] && maxx[p+1][n]==n)) 70 { 71 for(int k=p;k>j;k--) 72 { 73 if(f[k][p] && minx[k][p]==i) 74 { 75 // cout<<i<<" "<<j<<" "<<k<<" "<<p<<":"<<f[1][i-1]+(k-1>=j+1?f[j+1][k-1]:0)+f[p+1][n]+2<<endl; 76 ans=max(ans,f[1][i-1]+(k-1>=j+1?f[j+1][k-1]:0)+f[p+1][n]+2); 77 } 78 } 79 } 80 } 81 ans=max(ans,f[1][n]); 82 printf("%d ",ans); 83 } 84 return 0; 85 }
Funny Function
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1016 Accepted Submission(s): 491
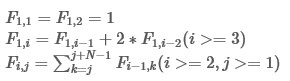
For given integers N and M,calculate F
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define mod 1000000007 4 #define LL long long 5 using namespace std; 6 LL n,m,ans; 7 LL quick_pow(LL i,LL n) 8 { 9 LL res=1,mul=(i%mod+mod)%mod; 10 while(n) 11 { 12 if(n%2==1) 13 res=(res*mul)%mod; 14 mul=(mul*mul)%mod; 15 n/=2; 16 } 17 return res; 18 } 19 void exgcd(LL a,LL b,LL &x,LL &y,LL &gcd) 20 { 21 if(!b) {gcd=a; x=1; y=0; } 22 else {exgcd(b,a%b,y,x,gcd); y-=x*(a/b); } 23 return ; 24 } 25 int main() 26 { 27 int T; 28 LL x,y,gcd; 29 scanf("%d",&T); 30 for(int kase=1;kase<=T;kase++) 31 { 32 scanf("%lld%lld",&n,&m); 33 ans=(quick_pow((quick_pow(2,n)-1),m-1)*2%mod+(n%2==1?1:0)+mod)%mod; 34 exgcd(3,mod,x,y,gcd); 35 x=(x%mod+mod)%mod; 36 ans=(ans*(LL)x)%mod; 37 printf("%lld ",ans); 38 } 39 return 0; 40 }
To my boyfriend
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 630 Accepted Submission(s): 289
I never forget the moment I met with you. You carefully asked me: "I have a very difficult problem. Can you teach me?". I replied with a smile, "of course". You replied:"Given a matrix, I randomly choose a sub-matrix, what is the expectation of the number of **different numbers** it contains?"
Sincerely yours,
Guo
Each case contains two integers, n and m (1≤n, m≤100), the number of rows and the number of columns in the grid, respectively.
The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains g_i,j (0≤ g_i,j < n*m).

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define LL long long 4 using namespace std; 5 int maped[110][110]; 6 int last[10010][110],inlast[110]; 7 long double ans; 8 stack< pair<int,int> > pushlas,by; 9 int max(int a,int b) 10 { 11 return a>b?a:b; 12 } 13 int main() 14 { 15 int T,n,m,t,color,inlas,ct; 16 LL ans; 17 scanf("%d",&T); 18 for(int kase=1;kase<=T;kase++) 19 { 20 scanf("%d%d",&n,&m); 21 for(int i=1;i<=n;i++) 22 for(int j=1;j<=m;j++) 23 scanf("%d",&maped[i][j]); 24 clr(last); 25 ans=0; 26 for(int i=1;i<=n;i++) 27 for(int j=1;j<=m;j++) 28 { 29 t=0; 30 inlas=0; 31 color=maped[i][j]; 32 for(int k=m;k>=j;k--) 33 { 34 while(!by.empty() && last[color][k]>=by.top().first) 35 by.pop(); 36 by.push(make_pair(last[color][k],k)); 37 } 38 while(!by.empty()) 39 { 40 pushlas.push(by.top()); 41 by.pop(); 42 } 43 inlas=0; 44 for(int k=j;k>=1;k--) 45 { 46 inlas=max(inlas,last[color][k]); 47 inlast[k]=inlas; 48 } 49 inlas=m+1; 50 ct=0; 51 for(int k=1;k<=j;k++) 52 { 53 while(pushlas.top().first>inlast[k]) 54 { 55 ans+=(LL)(ct+(i-pushlas.top().first)*(j-k+1))*(LL)(inlas-pushlas.top().second)*(LL)(n-i+1); 56 inlas=pushlas.top().second; 57 pushlas.pop(); 58 } 59 ct+=i-inlast[k]; 60 } 61 ans+=(LL)ct*(inlas-pushlas.top().second)*(LL)(n-i+1); 62 pushlas.pop(); 63 last[color][j]=i; 64 } 65 printf("%0.9lf ",(double)ans/((n+1)*n*(m+1)*m)*4); 66 } 67 return 0; 68 }
TrickGCD
Time Limit: 5000/2500 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1996 Accepted Submission(s): 778
* 1≤B
* For each pair( l , r ) (1≤l≤r≤n
Each test case begins with an integer number n describe the size of array A
Then a line contains n
You can assume that 1≤n,A

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clrmax(x) memset(x,0,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 using namespace std; 7 int inf[100050],mu[100050]; 8 int prime[100050]; 9 int a[100050],sum[100050]; 10 int n,m,pcnt,ct,minai,maxai; 11 LL ans,sing; 12 void tooprimer(int n) 13 { 14 clr(inf); 15 pcnt=0; 16 for(int i=2;i<=n;i++) 17 { 18 if(!inf[i]) 19 { 20 prime[++pcnt]=i; 21 inf[i]=1; 22 mu[i]=1; 23 } 24 for(int j=1;j<=pcnt;j++) 25 { 26 if(i*prime[j]>n) break; 27 inf[i*prime[j]]=1; 28 if(i%prime[j]==0) 29 { 30 mu[i*prime[j]]=0; 31 break; 32 } 33 else 34 mu[i*prime[j]]=-mu[i]; 35 } 36 } 37 return ; 38 } 39 LL quick_pow(LL i,LL n) 40 { 41 LL res=1,mul=(LL)i; 42 while(n) 43 { 44 if(n&1) 45 res=(res*mul)%mod; 46 mul=(mul*mul)%mod; 47 n>>=1; 48 } 49 return res; 50 } 51 52 inline int min(int &a,int &b) 53 { 54 return a<b?a:b; 55 } 56 inline int max(int &a,int &b) 57 { 58 return a>b?a:b; 59 } 60 int main() 61 { 62 tooprimer(100000); 63 int T,sqr; 64 scanf("%d",&T); 65 for(int kase=1;kase<=T;kase++) 66 { 67 minai=0x3f3f3f3f; 68 maxai=0; 69 scanf("%d",&n); 70 clr(sum); 71 for(int i=1;i<=n;i++) 72 { 73 scanf("%d",&a[i]); 74 sum[a[i]]++; 75 minai=min(a[i],minai); 76 maxai=max(a[i],maxai); 77 } 78 for(int i=1;i<=maxai;i++) 79 sum[i]=sum[i-1]+sum[i]; 80 ans=0; 81 for(int i=2;i<=maxai;i++) 82 { 83 sing=1; 84 if(mu[i]==0) 85 continue; 86 if(sum[i-1]>0) 87 continue; 88 for(int j=i;j<=maxai;j+=i) 89 { 90 sing=sing*quick_pow((LL)(j/i),(LL)(sum[(j+i-1>maxai?maxai:j+i-1)]-sum[j-1]))%mod; 91 } 92 ans=((ans+sing*(LL)mu[i])%mod+mod)%mod; 93 } 94 printf("Case #%d: %lld ",kase,ans); 95 } 96 return 0; 97 }
Regular polygon
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1959 Accepted Submission(s): 776
整数点对应的正多边形只有正方形。看透这点这题就是水题了。枚举所有边求有没有对应的正方形即可。记得去除重复的正方形。

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clrmax(x) memset(x,0,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 #define come 210 7 using namespace std; 8 bool mapped[800][800]; 9 struct node 10 { 11 int x,y; 12 }pt[1000]; 13 int main() 14 { 15 int T,n,m,k,l,maxx,ct,xi,yi,lenk,lenl,t,ans; 16 LL p; 17 while(scanf("%d",&n)!=EOF) 18 { 19 clr(mapped); 20 for(int i=1;i<=n;i++) 21 { 22 scanf("%d%d",&pt[i].x,&pt[i].y); 23 pt[i].x+=come; 24 pt[i].y+=come; 25 mapped[pt[i].x][pt[i].y]=1; 26 } 27 ans=0; 28 for(int i=1;i<=n;i++) 29 for(int j=1;j<=n;j++) 30 if(i!=j) 31 { 32 yi=-(pt[i].x-pt[j].x); 33 xi=pt[i].y-pt[j].y; 34 if(xi+pt[i].x>0 && yi+pt[i].y>0 && mapped[xi+pt[i].x][yi+pt[i].y]==1 && xi+pt[j].x>0 && yi+pt[j].y>0 && mapped[xi+pt[j].x][yi+pt[j].y]==1) 35 ans++; 36 xi=-xi; 37 yi=-yi; 38 if(xi+pt[i].x>0 && yi+pt[i].y>0 && mapped[xi+pt[i].x][yi+pt[i].y]==1 && xi+pt[j].x>0 && yi+pt[j].y>0 && mapped[xi+pt[j].x][yi+pt[j].y]==1) 39 ans++; 40 } 41 printf("%d ",ans/8); 42 } 43 return 0; 44 }
