第一个是 pick 定律 任意多边形的面积;如果他的顶点是整数点的话; 他的面积 s 等于 他边长上整数点的个数的一半 + 他包含的整数点个数;
x + y = n ( n 是一个素数 ) 那么
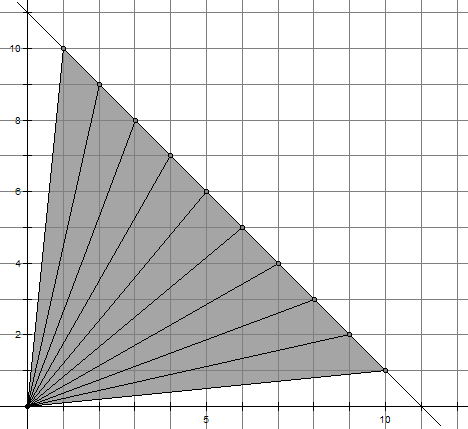
考虑直线x+y=n,其中n是一个素数。这条直线将恰好通过第一象限里的n-1个格点(如上图,图中所示的是n=11的情况)。将这n-1个点分别和原点相连,于是得到了n-2个灰色的三角形。仔细数数每个三角形内部的格点数,你会发现一个惊人的事实:每个三角形内部所含的格点数都是一样多。这是为什么呢?
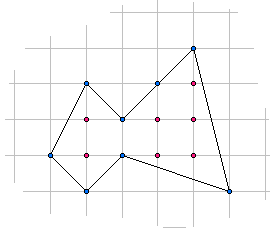
Pick定理是说,在一个平面直角坐标系内,如果一个多边形的顶点全都在格点上,那么这个图形的面积恰好就等于边界上经过的格点数的一半加上内部所含格点数再减一。例如,上图多边形的边界上有8个格点,内部含有7个格点,那么其面积就等于8/2+7-1=10。我们曾经在这里看到过一个非常神奇非常诡异的证明。这个定理有一些非常巧妙的应用。在上面的问题里,所有三角形都是等底等高的,因此它们的面积都相等。另外,注意到x与y的和是一个素数,这表明x和y是互素的(否则x+y可以提出一个公因数d,与和为素数矛盾),也就是说(x,y)和原点的连线不会经过其它格点。既然所有三角形的面积都相等,边界上的格点数也相等,由Pick定理,我们就能直接得出每个三角形内部的格点数也相等了。
x 和 y 互质 则他们与原点的连线不会出现整数点 证明过程
(x,y) 与 ( x-a,y-a )== (c,d ) 平行;
则 点积 x×c = y×d
则 x/y = d/c; x 与 y 互质
则 d = k * x;
c = k * y; k < 1;
则 不为 整数;~~