POJ 1279 Art Gallery (半平面交)

题目链接：POJ 1279

Problem Description

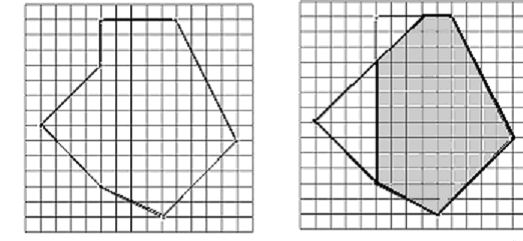
The art galleries of the new and very futuristic building of the Center for Balkan Cooperation have the form of polygons (not necessarily convex). When a big exhibition is organized, watching over all of the pictures is a big security concern. Your task is that for a given gallery to write a program which finds the surface of the area of the floor, from which each point on the walls of the gallery is visible. On the figure 1. a map of a gallery is given in some co-ordinate system. The area wanted is shaded on the figure 2.

Input

The number of tasks T that your program have to solve will be on the first row of the input file. Input data for each task start with an integer N, 5 <= N <= 1500. Each of the next N rows of the input will contain the co-ordinates of a vertex of the polygon ? two integers that fit in 16-bit integer type, separated by a single space. Following the row with the co-ordinates of the last vertex for the task comes the line with the number of vertices for the next test and so on.

Output

For each test you must write on one line the required surface - a number with exactly two digits after the decimal point (the number should be rounded to the second digit after the decimal point).

Sample Input

1
7
0 0
4 4
4 7
9 7
13 -1
8 -6
4 -4

Sample Output

80.00

Source

Southeastern Europe 2002

Solution

题意

给定 (n) 个点的多边形，求多边形的核的面积。

题解

半平面交

半平面交求多边形的核的模板题。注意给出点的顺序是顺时针的，要处理一下。

Code

#include <cstdio>
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef double db;
const db eps = 1e-10;  
const db pi = acos(-1.0);  
const ll inf = 0x3f3f3f3f3f3f3f3f;  
const ll maxn = 1e3 + 10;

inline int dcmp(db x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}

class Point {
public:
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    inline void input() {
        scanf("%lf%lf", &x, &y);
    }
    bool operator<(const Point &a) const {
        return (!dcmp(x - a.x))? dcmp(y - a.y) < 0: x < a.x;
    }
    bool operator==(const Point &a) const {
        return dcmp(x - a.x) == 0 && dcmp(y - a.y) == 0;
    }
    db dis2(const Point a) {
        return pow(x - a.x, 2) + pow(y - a.y, 2);
    }
    db dis(const Point a) {
        return sqrt(dis2(a));
    }

    db dis2() {
        return x * x + y * y;
    }
    db dis() {
        return sqrt(dis2());
    }
    Point operator+(const Point a) {
        return Point(x + a.x, y + a.y);
    }
    Point operator-(const Point a) {
        return Point(x - a.x, y - a.y);
    }
    Point operator*(double p) {
        return Point(x * p, y * p);
    }
    Point operator/(double p) {
        return Point(x / p, y / p);
    }
    db dot(const Point a) {
        return x * a.x + y * a.y;
    }
    db cross(const Point a) {
        return x * a.y - y * a.x;
    }
    db ang(Point a) {
        return acos((a.dis() * dis()) / dot(a));
    }
};
typedef Point Vector;

Point p[maxn], ip[maxn];

class Line {
public:
    Point s, e;
    db angle;
    Line() {}
    Line(Point s, Point e) : s(s), e(e) {}
    inline void input() {
        s.input();e.input();
    }
    bool operator<(const Line &a) const {
        Line l = a;
        if(dcmp(angle - l.angle) == 0) {
            return l.toLeftTest(s) == 1;
        }
        return angle < l.angle;
    }
    void get_angle() {
        angle = atan2(e.y - s.y, e.x - s.x);
    }
    int toLeftTest(Point p) {
        if((e - s).cross(p - s) > 0) return 1;
        else if((e - s).cross(p - s) < 0) return -1;
        return 0;
    }
    int linecrossline(Line l) {
        if(dcmp((e - s).cross(l.e - l.s)) == 0) {
            if(dcmp((l.s - e).cross(l.e - s)) == 0) {
                return 0;
            }
            return 1;
        }
        return 2;
    }
    Point crosspoint(Line l) {
		db a1 = (l.e - l.s).cross(s - l.s);
		db a2 = (l.e - l.s).cross(e - l.s);
        db x = (s.x * a2 - e.x * a1) / (a2 - a1);
        db y = (s.y * a2 - e.y * a1) / (a2 - a1);
        if(dcmp(x) == 0) x = 0;
        if(dcmp(y) == 0) y = 0;
		return Point(x, y);
	}
};

Line l[maxn], q[maxn];

db half_plane(int cnt) {
    sort(l + 1, l + 1 + cnt);
    int tmp = 1;
    for(int i = 2; i <= cnt; ++i) {
        if(dcmp(l[i].angle - l[tmp].angle) == 1) l[++tmp] = l[i];
    }
    cnt = tmp;
    int head = 1, tail = 2;
    q[1] = l[1], q[2] = l[2];
    for(int i = 3; i <= cnt; ++i) {
        while(head < tail && l[i].toLeftTest(q[tail].crosspoint(q[tail - 1])) == -1) {
            --tail;
        }
        while(head < tail && l[i].toLeftTest(q[head].crosspoint(q[head + 1])) == -1) {
            ++head;
        }
        q[++tail] = l[i];
    }

    while(head < tail && q[head].toLeftTest(q[tail].crosspoint(q[tail - 1])) == -1) {
        --tail;
    }
    while(head < tail && q[tail].toLeftTest(q[head].crosspoint(q[head + 1])) == -1) {
        ++head;
    }

    if(tail - head + 1 <= 2) {
        return 0.0;
    }

    tmp = 0;
    for(int i = head; i < tail; ++i) {
        ip[++tmp] = q[i].crosspoint(q[i + 1]);
    }
    ip[++tmp] = q[head].crosspoint(q[tail]);
    db ans = 0;
    for(int i = 3; i <= tmp; ++i) {
        ans += (ip[i - 1] - ip[1]).cross(ip[i] - ip[1]);
    }
    return ans * 0.5;
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        int n;
        scanf("%d", &n);
        int cnt = 0;
        for(int i = 1; i <= n; ++i) {
            p[i].input();
        }
        for(int i = n - 1; i >= 1; --i) {
            l[++cnt].e = p[i];
            l[cnt].s = p[i + 1];
            l[cnt].get_angle();
        }
        l[++cnt].e = p[n];
        l[cnt].s = p[1];
        l[cnt].get_angle();
        printf("%.2lf
", half_plane(cnt));
    }
    return 0;
}