网络流初步最大流

　　网络流 (Network Flow) 是指在一个每条边都有容量 (Capacity) 的有向图分配流，使一条边的流量不会超过它的容量。（边有附带容量的图称为网络）一道流必须符合一个结点的进出的流量相同的限制，除非这是一个源点 (Source) ──有较多向外的流；或是一个汇点 (Sink) ──有较多向内的流。一个网络可以用来模拟道路系统的交通量、管中的液体、电路中的电流或类似一些东西在一个结点的网络中游动的任何事物。

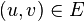　　设 是一个有限的有向图，它的每条边 都有一个非负值实数的容量 。如果 ，我们假设 。我们区别两个顶点：一个源点 和一个汇点 。一道网络流是一个对于所有结点 和 都有以下特性的实数函数 ：

容量限制 (Capacity Constraints)：	一条边的流不能超过它的容量。
斜对称 (Skew Symmetry)：	由 到 的净流必须是由 到 的净流的相反（参考例子）。
流守恒 (Flow Conservation)：	除非或，否则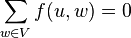 一结点的净流是零，除了“制造”流的源点和“消耗”流的汇点。

　　边的剩余容量 (Residual Capacity) 是 。这定义了以 表示的剩余网络 (Residual Network)，它显示可用的容量的多少。留意就算在原网络中由 到 没有边，在剩余网络仍可能有由 到 的边。因为相反方向的流抵消，减少由 到 的流等于增加由 到 的流。增广路 (Augmenting Path) 是一条路径 ，而 、及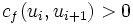，这表示沿这条路径传送更多流是可能的（既找一条从s到t的路径，路径上边的剩余容量都不为0）。

 【增广路求最大流算法】

　　在网络中找到一条增广路，路径上剩余容量最小的为d，把路径上所有边的流量都+d，显然操作后依旧满足上面的3条性质。只要网络中存在增广路，网络的流量就可以增加。如果不存在增广路，则当前流是最大流。

【Edmonds-Karp】

　　这个算法写的比较简洁，是用BFS来找增广路径的，防止一些数据会卡DFS。
       算法复杂度为O(VE²),适合节点多边少的网络，如果要求解边多的网络，则要用Dinic算法: O(V²E)

/*
    数组a[i]表示从路径起点到i点的最小剩余量
    数组p[u]记录路径中到达u点的前一个点
    f[u][v]表示从u到v的实际流量，要保证当前网络中的流量满足3个性质才能执行算法，最好都清0吧。
*/   
    queue<int> q;
    int sum=0;
    while (true)
    {
       memset(a,0,sizeof a);
       a[s]=MAXINT;  //s为起点，初始化防止被更新
       q.push(s);
       while (!q.empty())
       {
           int u=q.front();q.pop();
           for (int v=1;v<=n;++v)
            if (!a[v] && c[u][v]>f[u][v])
           {
               p[v]=u;  q.push(v);
               int t=c[u][v]-f[u][v];
               a[v]=a[u]<t?a[u]:t;
           }
       }
       if (a[t]==0) break;
       for (int u=t;u!=s;u=p[u])
       {
           f[p[u]][u]+=a[t];
           f[u][p[u]]-=a[t];
       }
        sum+=a[t];   //更新网络总流量
    }

　　代码中的BFS部分有点意思，由于数组a总是正数（c[u][v]>f[u][v]）,所以可以当做标记是否该点被访问过。BFS中所有点只被更新一次，如果第一次访问该点无法到达t，则再多次访问也没用,所以效率还是蛮高的。

【HDU 3549】

　　最大流的最基本题。

#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;
int n,m;
int c[20][20];
int f[20][20];
int work()
{
    int p[50];
    queue<int> q;
    int sum=0;
    int a[20];
    while (true)
    {
       memset(a,0,sizeof a);
       a[1]=2000000;
       q.push(1);
       while (!q.empty())
       {
           int u=q.front();q.pop();
           for (int v=1;v<=n;++v)
            if (!a[v] && c[u][v]>f[u][v])
           {
               p[v]=u;q.push(v);
               int t=c[u][v]-f[u][v];
               a[v]=a[u]<t?a[u]:t;
           }
       }
       if (a[n]==0) break;
       for (int u=n;u!=1;u=p[u])
       {
           f[p[u]][u]+=a[n];
           f[u][p[u]]-=a[n];
       }
        sum+=a[n];
    }
    return sum;
}
int main()
{
    int T;
    int cas=0;
    scanf("%d",&T);
    while (T--)
    {
        memset(c,0,sizeof c);
        memset(f,0,sizeof f);
        scanf("%d%d",&n,&m);
        for (int i=0;i<m;++i)
        {
            int x,y,t;
            scanf("%d%d%d",&x,&y,&t);
            c[x][y]+=t;
        }
        printf("Case %d: %d\n",++cas,work());
    }
}

 用最大流模板的代码：

#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;
int n,m;
class nstream
{
    static const int MAXINT=0x7fffffff;
    struct node
    {
        int n,c,f;
        int next;
        void set(int nn,int cc,int xx)
        {
            n=nn;   c=cc;
            next=xx;   f=0;
        }
    } *data;
    int *head,cnt,n,m;
    int *getf(int x,int y)
    {
        int ind=head[x];
        for (node *t; ind!=-1; ind=t->next)
        {
            t=&data[ind];
            if (t->n==y) return &t->f;
        }
        insert(x,y,0);
        return &data[head[x]].f;
    }
public:
    nstream(int nn,int mm):n(nn),m(mm)  //输入最大节点数和边数
    {
        data=new node[mm];
        head=new int[nn+2];
    }
    void clear()      //清理数据，初始化
    {
        for (int i=0;i<=n;++i) head[i]=-1;
        cnt=-1;
    }
    void insert(int x,int y,int k) // 把x到y的容量加k
    {
        int ind=head[x];
        for (node *t; ind!=-1; ind=t->next)
        {
            t=&data[ind];
            if (t->n==y)
            {
                t->c+=k;
                return;
            }
        }
        data[++cnt].set(y,k,head[x]);
        head[x]=cnt;
    }
    int work(int s,int t)  //计算从s 到t 的最大流
    {
        int p[50];
        queue<int> q;
        int sum=0;
        int a[25];
        while (true)
        {
            memset(a,0,sizeof a);
            a[s]=MAXINT;
            q.push(s);
            while (!q.empty())
            {
                int u=q.front();
                q.pop();
                node *t;
                for (int pp=head[u]; pp!=-1; pp=t->next)
                {
                    t=&data[pp];
                    int v=t->n;
                    if (!a[v] && t->c>t->f)
                    {
                        p[v]=u;
                        q.push(v);
                        int tt=t->c-t->f;
                        a[v]=a[u]<tt?a[u]:tt;
                    }
                }
            }
            if (a[t]==0) break;
            for (int u=t; u!=s; u=p[u])
            {
                (*getf(p[u],u))+=a[t];
                (*getf(u,p[u]))-=a[t];
            }
            sum+=a[t];
        }
        return sum;
    }
};

int main()
{
    int T;
    int cas=0;
    scanf("%d",&T);
    nstream my(20,20*23);
    while (T--)
    {
        my.clear();
        scanf("%d%d",&n,&m);
        for (int i=0; i<m; ++i)
        {
            int x,y,t;
            scanf("%d%d%d",&x,&y,&t);
            my.insert(x,y,t);
        }
        printf("Case %d: %d\n",++cas,my.work(1,n));
    }
}