OpenCVPython系列之Sobel和Scharr算子

我们再上个教程中留了一个小彩蛋——形态学的梯度问题，通常情况下，它被用于提取图像的轮廓，今天我们来了解图像边缘的另一种方法，它将比形态学梯度更有效，适用范围也更广。

Sobel算子

前面的例子，已经接触到了图像卷积运算。最终要的卷积运算之一是用于计算图像的导数（或近似导数）。为什么图像中导数的计算很重要，看下面边缘检测的例子：

很容易观察到上面图像中像素灰度值变化没有规律。一种比较好的描述这种变化的方法是采用导数。其中梯度剧烈变化的地方代表图像灰度值变化强烈的地方，也就是边缘。

为了更好的说明，以1维图像（也就是图像的1行）为例。边缘出现在灰度值跳变的地方，如下图所示：

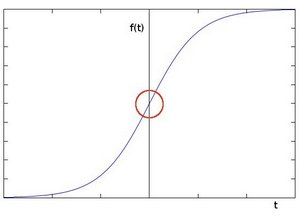
如果对上面的1维图像求导数，得到下图，可以很明显的看到边缘所在的位置。

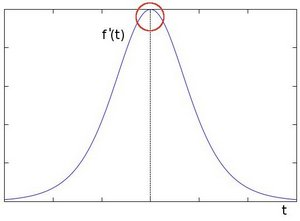
从上面的解释，我们可以设置一个阈值，根据局部像素变化强烈程度获取图像边缘。

sobel算子是一个离散微分算子，计算得到的是图像梯度的近似值。sobel算子结合了高斯平滑和微分。

假设输入图像是I，，核大小为3，通过下面运算分别计算水平方向和垂直方向的微分：

a.水平方向：

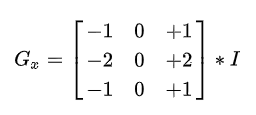
b.垂直方向：

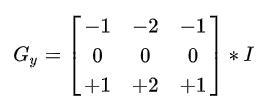
具体运算为：

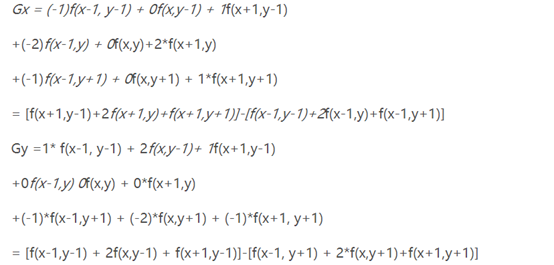
结合上面结果可以计算出图像中一个点的近似梯度：

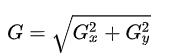
或者表示为：

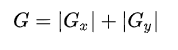
需要注意的是，当核的大小为3时，也就是上面所示的Sobel核可能会产生明显的误差(毕竟Sobel只是微分的近似值)。

在OpenCV-Python中，使用Sobel的算子的函数原型如下：

dst = cv2.Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]])

前四个是必须的参数：

第一个参数是需要处理的图像；

第二个参数是图像的深度，-1表示采用的是与原图像相同的深度。目标图像的深度必须大于等于原图像的深度；

dx和dy表示的是求导的阶数，0表示这个方向上没有求导，一般为0、1、2。

其后是可选的参数：

dst不用解释了；

ksize是Sobel算子的大小，必须为1、3、5、7。

scale是缩放导数的比例常数，默认情况下没有伸缩系数；

delta是一个可选的增量，将会加到最终的dst中，同样，默认情况下没有额外的值加到dst中；

borderType是判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。

现在我们来看实验图像：

实战代码：

import cv2
import numpy as np

img = cv2.imread("pie.png",0)
x = cv2.Sobel(img,cv2.CV_16S,1,0)

cv2.imshow("x",x)

cv2.waitKey(0)
cv2.destroyAllWindows()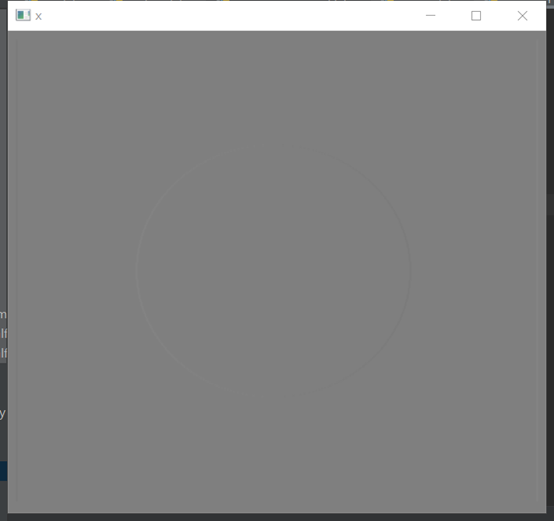

我们发现没有输出，原因在于图像格式的问题，在Sobel函数的第二个参数这里使用了cv2.CV_16S。因为OpenCV文档中对Sobel算子的介绍中有这么一句：“in the case of 8-bit input images it will result in truncated derivatives”。即Sobel函数求完导数后会有负值，还有会大于255的值。而原图像是uint8，即8位无符号数，所以Sobel建立的图像位数不够，会有截断。因此要使用16位有符号的数据类型，即cv2.CV_16S。

在经过处理后，别忘了用convertScaleAbs()函数将其转回原来的uint8形式。否则将无法显示图像，而只是一副灰色的窗口。convertScaleAbs()的原型为：

dst = cv2.convertScaleAbs(src[, dst[, alpha[, beta]]])

其中可选参数alpha是伸缩系数，beta是加到结果上的一个值。结果返回uint8类型的图片。

由于Sobel算子是在两个方向计算的，最后还需要用cv2.addWeighted(...)函数将其组合起来。其函数原型为：

dst = cv2.addWeighted(src1, alpha, src2, beta, gamma[, dst[, dtype]])

当然，这个函数我们在前面已经讲述过在这里就不多讲述了。

我们再来看代码：

import cv2
import numpy as np

img = cv2.imread("pie.png",0)
x = cv2.Sobel(img,cv2.CV_16S,1,0)
y = cv2.Sobel(img,cv2.CV_16S,0,1)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)

dst = cv2.addWeighted(absX,0.5,absY,0.5,0)
cv2.imshow("x",absX)
cv2.imshow("y",absY)
cv2.imshow("res",dst)

cv2.waitKey(0)
cv2.destroyAllWindows()

先分别来看下，x，y两个方向上的：

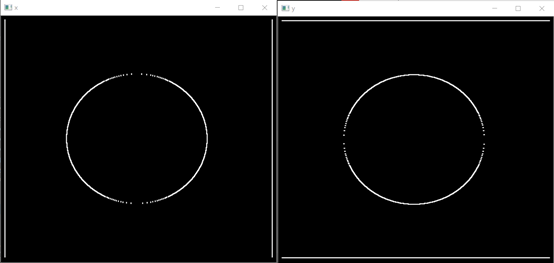
再看看最终相加在一起的：

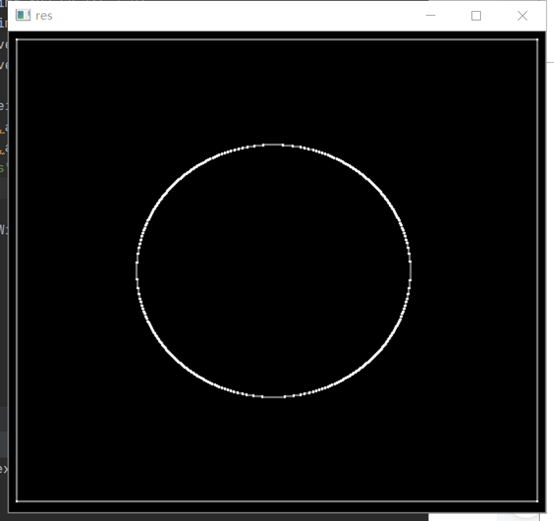
由于Sobel算子是滤波算子的形式，用于提取边缘，可以利用快速卷积函数， 简单有效，因此应用广泛。美中不足的是，Sobel算子并没有将图像的主体与背景严格地区分开来，即Sobel算子没有严格地模拟人的视觉生理特征，所以提取的图像轮廓有时并不能令人满意。

Scharr算子

Scharr() 函数提供了比标准Sobel函数更精确的计算结果。它使用了下面的核：

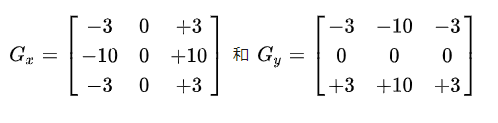
除了卷积核与Sobel不同，在其余方面它与Sobel基本一致，我们来看它的函数原型：

dst = cv2.Scharr(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]])

参数就不再介绍了，与Sobel是完全一致的，我们来看看代码演示：

import cv2
import numpy as np

img = cv2.imread("pie.png",0)
x = cv2.Scharr(img,cv2.CV_16S,1,0)
y = cv2.Scharr(img,cv2.CV_16S,0,1)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)

dst = cv2.addWeighted(absX,0.5,absY,0.5,0)
cv2.imshow("res",dst)

cv2.waitKey(0)
cv2.destroyAllWindows()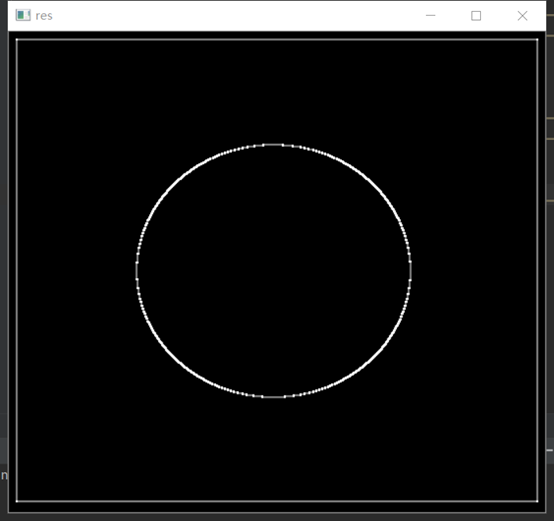

本次教程所讲述的Sobel算子与Scharr算子在图形的边缘检测方面有些缺陷，想必大家也看到了，不过在下次教程我们将会讲述这个问题。