偏差和方差
在学习Ridge和Lasso之前,我们先看一下偏差和方差的概念。
机器学习算法针对特定数据所训练出来的模型并非是十全十美的,再加上数据本身的复杂性,误差不可避免。说到误差,就必须考虑其来源:模型误差 = 偏差(Bias)+ 方差(Variance)+ 数据本身的误差。其中数据本身的误差,可能由于记录过程中的一些不确定性因素等导致,这个我们无法避免,能做的只有不断优化模型参数来权衡偏差和方差,使得模型误差尽可能降到最低。
偏差:导致偏差的原因有多种,其中一个就是针对非线性问题使用线性方法求解,当模型欠拟合时,就会出现较大的偏差
方差:产生高方差的原因通常是由于模型过于复杂,即模型过拟合时,会出现较大的方差
通常情况下,我们降低了偏差就会相应地使得方差提高,降低了方差就会相应地提高了偏差,所以在机器学习的模型中,我们总是希望找到一组最优的参数,这些参数能权衡模型的偏差和方差,使得模型性能达到最优。我在知乎上找到这样一张图方便各位理解。

岭回归(Ridge)
针对高方差,即过拟合的模型,解决办法之一就是对模型进行正则化:限制参数大小(由于本篇博客所提到的岭回归和Lasso都是正则化的特征选择方法,所以对于其他解决过拟合的方法不多赘述)当线性回归过拟合时,权重系数wj就会非常的大,岭回归就是要解决这样的问题。岭回归(Ridge Regression)可以理解为在线性回归的损失函数的基础上,加,入一个L2正则项,来限制W不要过大。其中λ>0,通过确定λ的值可以使得模型在偏差和方差之间达到平衡,随着λ的增大,模型的方差减小,偏差增大。
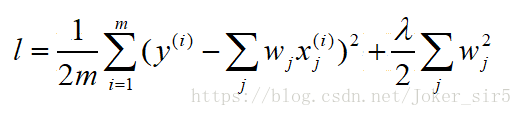
我们可以像线性回归一样,利用最小二乘法求解岭回归模型的参数,对W求导,令倒数等于0,可求得W的解析解,其中I为m x m的单位矩阵,所以也可以说岭回归就是在矩阵X^TX上加一个λI使得矩阵非奇异,进而能对XTX+λI求逆:
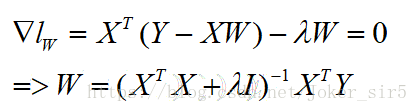
套索回归(Lasso)
Lasso回归和岭回归类似,不同的是,Lasso可以理解为在线性回归基础上加入一个L1正则项,同样来限制W不要过大。其中λ>0,通过确定λ的值可以使得模型在偏差和方差之间达到平衡,随着λ的增大,模型的方差减小,偏差增大。
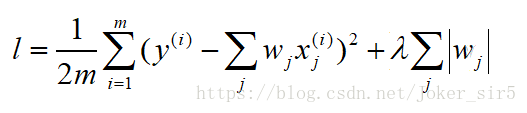
Lasso趋向于使得一部分w值变为0,所以可以作为特征选择用,因为这里的L1正则项并不是处处可导的,所以并不能直接使用基于梯度的方法优化损失函数,若要从底层实现,可以使用拟牛顿法的BFGS算法,逐步向前回归,我这里直接用sklearn封装的Lasso,请参见

总结
Lasso由于使用L1正则项,所以具有一定的特征选择功能,因为L1正则倾向于产生稀疏稀疏,它可以将一些“对标签没有用处”的特征对应的系数压缩为0,进而将对结果有较大影响的特征突显出来,而岭回归中L2正则项不具备这个功能,它只会讲一些无关特征的系数降到一个较小的值,但不会降为0。并且L2正则有解析解,L1没有,所以还有一种对岭回归和Lasso折中的方法------弹性网络(Elastic Net)
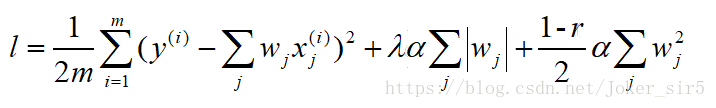
转载于:https://blog.csdn.net/Joker_sir5/article/details/82756089
原作者:Joker_sir5