压缩感知（CompressiveSensing, or Compressed Sensing）或译为压缩传感，或者称为压缩采样（Compressive sampling），以下统称压缩感知，简称CS。
在压缩感知的有关文献中几乎都在说“压缩感知突破了传统的Nquist/Shannon抽样定理的限制，它摒弃了传统压缩系统先以Nyquist采样速率采样再压缩的方法，而是边采样边压缩，即实现的不再是模拟数字转换(ADC)，而是模拟信息转换(AIC)”。
Nyquist/Shannon抽样定理：
抽样定理是由奈奎斯特(Nyquist)和香农(Shannon)分别于1928年和1949年提出的，所以又称为奈奎斯特抽样定理或香农抽样定理。
注：以上内容摘自“胡广书. 数字信号处理——理论算法与实现（第二版）[M]. 北京：清华大学出版社，2003.”
依照以上叙述，这里我给出压缩感知抽样定理的内容（CS抽样定理）：
对比Nyquist抽样定理和CS抽样定理，我们会发现：Nyquist抽样定理的前提是“信号x(t)是有限带宽的，其频谱的最高频率为fc”，而CS抽样定理的前提是“信号x(t)可以在某变换域稀疏表示，其稀疏度为K”，因此并不是CS抽样定理突破了Nyquist抽样定理的限制，而是其信号能够重建的依据（K稀疏）与Nyquist抽样定理（带限）的不同，我们可以展开遐想：信号抽样时我们即不以带限为前提也不以K稀疏为前提，而是基于一个其它合理的前提，那么也许可以提出更加有效的新抽样定理。
compressive sensing(CS)又称compressived sensing，compressived sample，大意是在采集信号的时候（模拟到数字），同时完成对信号压缩，中文翻译成压缩感知，意思变得至少不太好理解了。理论本身是“通过对信号的高度不完备线性测量的高精确的重建”
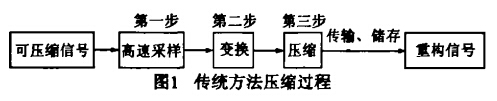
老式压缩原理：把原始图像表示为不同“小波”的线性叠加，记录显著的（高强度的）小波的系数，放弃掉（或者用阈值排除掉）剩下的小波系数。
总体来讲，原始的1024×2048图像可能含有两百万自由度，想要用小波来表示这个图像的人需要两百万个不同小波才能完美重建。但是典型的有意义的图像，从小波理论的角度看来是非常稀疏的，也就是可压缩的：可能只需要十万个小波就已经足够获取图像所有的可见细节了，其余一百九十万小波只贡献很少量的，大多数观测者基本看不见的“随机噪声”。（这也不是永远适用：含有大量纹理的图像–比如毛发、毛皮的图像——用小波算法特别难压缩，也是图像压缩算法的一大挑战。）
接下来呢，如果我们（或者不如说是相机）事先知道两百万小波系数里面哪十万个是重要的，那camera就可以只计算这十万个系数，别的就不管了。（对于单个系数的计算，可以在图像上应用一种合适的filter“滤波器”或叫mask“滤镜/掩模”，然后计量过滤出来的每个像素的色彩强度）但是，相机是不会知道哪个系数是重要的，所以它只好计量全部两百万个像素，把整个图像转换成基本小波，找出需要留下的那十万个主导基本小波，再删掉其余的。（这当然只是真正的图像压缩算法的一个草图，不过为了便于讨论我们还是就这么用吧。）
假设已知主要的小波系数，则有两种可行的手段来恢复数据：
•匹配追踪：找到一个其标记看上去与收集到的数据相关的小波；在数据中去除这个标记的所有印迹；不断重复直到我们能用小波标记“解释”收集到的所有数据。
Matching pursuit: locate a wavelet whose signature seems to correlate with the data collected; remove all traces of that signature from the data; and repeat until we have totally “explained” the data collected in terms of wavelet signatures. 就是先找出一个貌似是基的小波，然后去掉该小波在图像中的分量，迭代直到找出所有10w个小波.
•基追踪（又名L1模最小化）：在所有与(image)数据匹配的小波组合中，找到一个“最稀疏的”基，也就是其中所有系数的绝对值总和越小越好。（这种最小化的结果趋向于迫使绝大多数系数都消失了。）这种最小化算法可以利用单纯形法之类的凸规划算法，在合理的时间内计算出来。
Basis pursuit (or ![]()
minimisation): Out of all the possible combinations of wavelets which would fit the data collected, find the one which is “sparsest” in the sense that the total sum of the magnitudes of all the coefficients is as small as possible. (It turns out that this particular minimisation tends to force most of the coefficients to vanish.) This type of minimisation can be computed in reasonable time via convex optimisationmethods such as the simplex method.
参考来源：