压缩感知重构算法之子空间追踪(SP)

SP的提出时间比CoSaMP提出时间稍晚一些，但和压缩采样匹配追踪(CoSaMP)的方法几乎是一样的。SP与CoSaMP主要区别在于“In each iteration, in the SP algorithm, only K new candidates are added, while theCoSAMP algorithm adds 2K vectors.”，即SP每次选择K个原子，而CoSaMP则选择2K个原子；这样带来的好处是“This makes the SP algorithm computationally moreefficient,”。

在看代码之前，先看了SP的论文[1]，在摘要部分提到SP算法具有两个主要特点：一是较低的计算复杂度，特别是针对比较稀疏的信号的重构时，相比OMP算法，SP算法具有更低的计算复杂度；二是具有和线性规划优化（LP）方法相近的重构精度。在待重构信号具有比较小的稀疏度的情况下，SP的计算复杂度明显比LP方法的小，但是重构质量比LP的差。

在论文中还提到这么一段与OMP方法的比较，并提供了图形加以理解。SP方法和OMP方法最大的区别就是针对所选择的原子有无回溯（反向跟踪）。

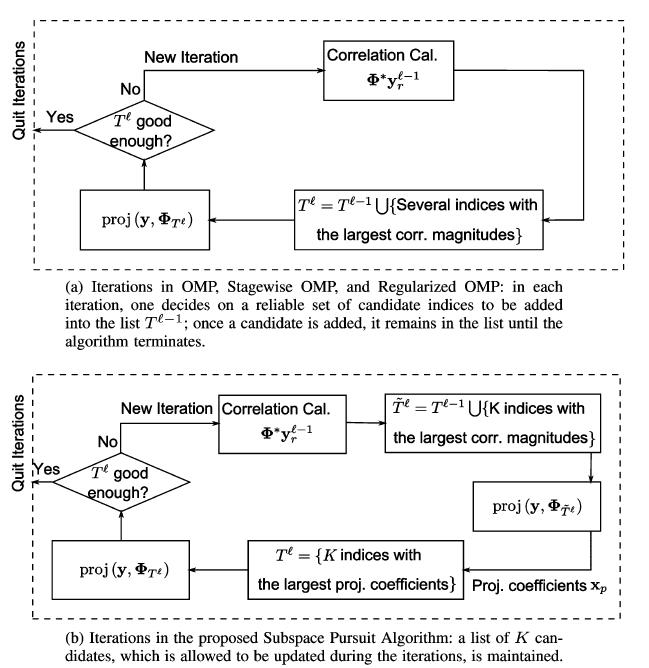
参考文献[2]中对SP算法进行了解释，如下所示：

在论文中还提到这么一段与OMP方法的比较，并提供了图形加以理解。SP方法和OMP方法最大的区别就是针对所选择的原子有无回溯（反向跟踪）。

以下是文献[1]中的给出的SP算法流程：

这个算法流程的初始化(Initialization)其实就是类似于CoSaMP的第1次迭代，注意第(1)步中选择了K个原子：“K indices corresponding to the largest magnitude entries”，在CoSaMP里这里要选择2K个最大的原子，后面的其它流程都一样。这里第(5)步增加了一个停止迭代的条件：当残差经过迭代后却变大了的时候就停止迭代。

鉴于SP与CoSaMP如此相似，这里不就再单独给出SP的步骤了，参考《压缩感知重构算法之压缩采样匹配追踪(CoSaMP)》，只需将第(2)步中的2K改为K即可。

function [ theta ] = CS_SP( y,A,K )
%CS_SP Summary of this function goes here 
%Version: 1.0 written by jbb0523 @2015-05-01 
%   Detailed explanation goes here 
%   y = Phi * x 
%   x = Psi * theta 
%   y = Phi*Psi * theta 
%   令 A = Phi*Psi, 则y=A*theta 
%   K is the sparsity level 
%   现在已知y和A，求theta 
%   Reference:Dai W，Milenkovic O．Subspace pursuit for compressive sensing 
%   signal reconstruction[J]．IEEE Transactions on Information Theory， 
%   2009，55(5)：2230-2249. 
    [y_rows,y_columns] = size(y); 
    if y_rows<y_columns 
        y = y';%y should be a column vector 
    end 
    [M,N] = size(A);%传感矩阵A为M*N矩阵 
    theta = zeros(N,1);%用来存储恢复的theta(列向量) 
    Pos_theta = [];%用来迭代过程中存储A被选择的列序号 
    r_n = y;%初始化残差(residual)为y 
    for kk=1:K%最多迭代K次 
        %(1) Identification 
        product = A'*r_n;%传感矩阵A各列与残差的内积 
        [val,pos]=sort(abs(product),'descend'); 
        Js = pos(1:K);%选出内积值最大的K列 
        %(2) Support Merger 
        Is = union(Pos_theta,Js);%Pos_theta与Js并集 
        %(3) Estimation 
        %At的行数要大于列数，此为最小二乘的基础(列线性无关) 
        if length(Is)<=M 
            At = A(:,Is);%将A的这几列组成矩阵At 
        else%At的列数大于行数，列必为线性相关的,At'*At将不可逆 
            break;%跳出for循环 
        end 
        %y=At*theta，以下求theta的最小二乘解(Least Square) 
        theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解 
        %(4) Pruning 
        [val,pos]=sort(abs(theta_ls),'descend'); 
        %(5) Sample Update 
        Pos_theta = Is(pos(1:K)); 
        theta_ls = theta_ls(pos(1:K)); 
        %At(:,pos(1:K))*theta_ls是y在At(:,pos(1:K))列空间上的正交投影 
        r_n = y - At(:,pos(1:K))*theta_ls;%更新残差  
        if norm(r_n)<1e-6%Repeat the steps until r=0 
            break;%跳出for循环 
        end 
    end 
    theta(Pos_theta)=theta_ls;%恢复出的theta 
end 

鉴于SP与CoSaMP的极其相似性，这里就不再给出单次重构和测量数M与重构成功概率关系曲线绘制例程代码了，只需将CoSaMP中调用CS_CoSaMP函数的部分改为调用CS_SP即可，无须任何其它改动。这里给出对比两种重构算法所绘制的测量数M与重构成功概率关系曲线的例程代码，只有这样才可以看出两种算法的重构性能优劣，以下是在分别运行完SP与CoSaMP的测量数M与重构成功概率关系曲线绘制例程代码的基础上，即已经存储了数据CoSaMPMtoPercentage1000.mat和SPMtoPercentage1000.mat：

clear all;close all;clc; 
load CoSaMPMtoPercentage1000; 
PercentageCoSaMP = Percentage; 
load SPMtoPercentage1000; 
PercentageSP = Percentage; 
S1 = ['-ks';'-ko';'-kd';'-kv';'-k*']; 
S2 = ['-rs';'-ro';'-rd';'-rv';'-r*']; 
figure; 
for kk = 1:length(K_set) 
    K = K_set(kk); 
    M_set = 2*K:5:N; 
    L_Mset = length(M_set); 
    plot(M_set,PercentageCoSaMP(kk,1:L_Mset),S1(kk,:));%绘出x的恢复信号 
    hold on;     
    plot(M_set,PercentageSP(kk,1:L_Mset),S2(kk,:));%绘出x的恢复信号 
end 
hold off; 
xlim([0 256]); 
legend('CoSaK=4','SPK=4','CoSaK=12','SPK=12','CoSaK=20',... 
    'SPK=20','CoSaK=28','SPK=28','CoSaK=36','SPK=36'); 
xlabel('Number of measurements(M)'); 
ylabel('Percentage recovered'); 
title('Percentage of input signals recovered correctly(N=256)(Gaussian)'); 

运行结果如下：

 

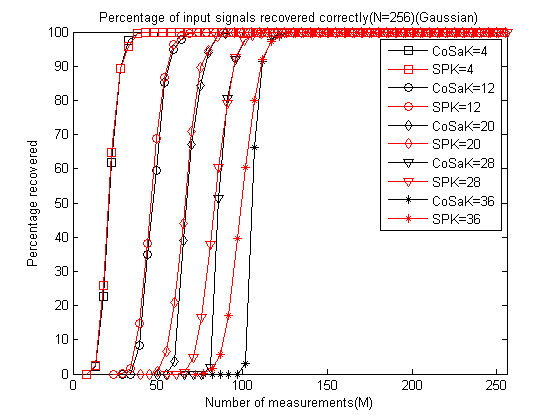
可以发现在M较小时SP略好于CoSaMP，当M变大时二者重构性能几乎一样。

 

参考文献：

[1] Dai W，Milenkovic O．Subspacepursuit for compressive sensing signal reconstruction[J]．IEEETransactions on Information Theory，2009，55(5)：2230-2249.

[2] 杨真真，杨震，孙林慧.信号压缩重构的正交匹配追踪类算法综述[J]. 信号处理，2013，29(4)：486-496.

[3] 彬彬有礼.压缩感知重构算法之子空间追踪(SP).http://blog.csdn.net/jbb0523/article/details/45441459