New Year Transportation
新年就要来了!在这个世界中,有n个单元格,它们的编号是从1到n,就像一个1×n板。人住在细胞里。然而,它很难在不同的细胞之间移动,因为很难逃离细胞。
人们想要认识住在其他牢房的人。因此,tncks0121用户制作了一个运输系统,在这些细胞之间移动,以庆祝新年。首先,他想到n - 1个正整数a 1, a 2,…, a n - 1。每个整数 i where 1 ≤ i ≤ n - 1 条件 1 ≤ a i ≤ n - i。
接下来,他制作了n - 1个入口,用从1到n - 1的整数进行编号。i _th(1≤i≤n - 1)门户连接单元i和单元(i + a i),可以使用i -th门户从单元i到单元(i + a i)。不幸的是,不能向后使用门户,这意味着不能使用i _th门户从单元格(i + a i)移动到单元格i。很容易看出,由于条件1≤ ai ≤ n -i,一个人不能使用门户离开线路世界。
目前我在1号牢房,我想去t牢房。然而,我不知道是否有可能去那里。请确定我是否可以只使用构造的运输系统去细胞t。
输入
//第一行是两个用空格分隔的整数n(3≤n≤3×104)和t(2≤t≤n)——我要去的单元格数量和单元格的索引。第二行包含n - 1个用空格分隔的整数a1, a2,…, an - 1 (1 ≤ ai ≤ n - i).这是可以保证的,使用给定的交通系统,一个人不能离开线的世界。
8 4
1 2 1 2 1 2 1
8 5
1 2 1 2 1 1 1
输出
//如果我可以使用运输系统进入t单元,打印“YES”。否则,打印“不”。
YES
NO
备注:
在第一个样本中,访问的细胞为:1、2、4;这样我们就能成功访问细胞4。
在第二个样本中,可能访问的细胞为:1、2、4、6、7、8;所以我们不能访问我们想访问的5号细胞。
C
#include<stdio.h>
int a[30000];
int main()
{
int n,t;
while(scanf("%d%d",&n,&t)!=EOF)
{
int flag=0;
for(int i=1;i<=n-1;i++)
{
scanf("%d",&a[i]);
}
for(int i=1;i<=n-1;)
{
if(i+a[i]==t)
{
flag=1;
break;
}
else
{
i=i+a[i];
}
}
if(flag)
printf("YES
");
else
printf("NO
");
}
return 0;
}
//https://blog.csdn.net/qq_34681949/article/details/52598351
C. Ice Skating
巴伊泰克正在学习滑冰。他是个新手,所以他唯一的交通方式就是从雪堆上向北、东、南、西滑动,直到他降落在另一个雪堆上。他已经注意到,用这种方式从一些积雪堆到另一些是不可能通过任何顺序的移动。他现在想堆一些额外的雪堆,这样他就可以从任何雪堆到任何其他雪堆。他让你找出需要制造的积雪的最小数量。我们假设Bajtek只能在整数坐标下堆积积雪。
示例
输入
//输入的第一行包含一个整数n(1≤n≤100)——积雪的数量。以下n行每一行包含两个整数xi和yi(1≤xi, yi≤1000)-第i个雪堆的坐标。注意,北方向coinсides Oy轴的方向,所以东方向coinсides牛轴的方向。所有雪堆的位置都是不同的。
2
2 1
1 2
2
2 1
4 1
输出
//输出需要创建的雪堆的最小数量,以便Bajtek能够从任何其他雪堆到达任何雪堆。
1
0
C
# include <stdio.h>
int pre[101];
struct node
{
int x, y;
}a[101];
void init(int n)
{
for(int i=0; i<=n; ++i)
pre[i] = i;
}
int find(int x)
{
if(x != pre[x])
pre[x] = find(pre[x]);
return pre[x];
}
int main()
{
int n;
while(~scanf("%d",&n))
{
init(n);
int ans = 0;
for(int i=0; i<n; ++i)
scanf("%d%d",&a[i].x, &a[i].y);
for(int i=0; i<n; ++i)
for(int j=i+1; j<n; ++j)
{
if(a[i].x==a[j].x || a[i].y == a[j].y)
{
int px = find(i);
int py = find(j);
if(px != py)
{
++ans;
pre[py] = px;
}
}
}
printf("%d
",n-1-ans);
}
return 0;
}
//https://blog.csdn.net/junior19/article/details/54989665
CodeForces 330B Road Construct
一个国家有n个城市。最初,该国没有道路。一天,国王决定修建一些连接成对城市的道路。可以以任何一种方式穿越道路。他希望以这样的方式建造这些道路,即通过最多两条道路横越每个城市都可以到达任何其他城市。您还会得到 m对城市-无法在这两对城市之间建造道路。
您的任务是构造仍满足上述条件的最小数量的道路。约束条件将确保这始终是可能的。
输入描述:
第一行包含两个整数n和m。然后是m条线,每条线由两个整数a_i和b_i(1≤a_i, b_i≤n, a_i≠b_i)组成,这意味着不可能修建一条连接城市a_i和b_i的道路。假设这些城市的编号是从1到n。保证每个城市对在输入中最多出现一次。
输出描述:
您应该在第一行中打印一个整数s:应该构建的道路的最小数量。然后是s线,每条s线由两个整数a_i和b_i(1≤a_i, b_i≤n, a_i≠b_i)组成,即在城市a_i和b_i之间修建道路。如果有多个解决方案,您可以打印其中的任何一个。
示例
输入
4 1
1 3
输出
3
1 2
4 2
2 3
这是一个可能的解决方案的例子:
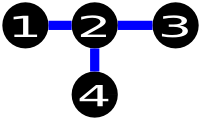
以下是一些错误解决方案的例子:
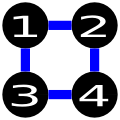
上面的解决方案是错误的,因为它没有使用最小的边数(4 vs 3)。此外,它还尝试在城市1和城市3之间建造一条道路,而输入指定不允许在城市1和城市3之间建造道路。
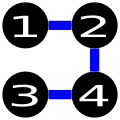
上述解决方案是错误的,因为从一个城市到另一个城市至少需要穿过3条路,而在你的国家,从任何一个城市到另一个城市至少需要穿过2条路。
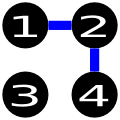
最后,上面的解决方案是错误的,因为从一个城市到另一个城市必须是可能的,而在这个国家不可能从城市1到3,从城市2到城市3,从城市4到城市3。
C
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
using namespace std;
int a[10010];
int main()
{
int n,m,x,y,i,cnt;
scanf("%d %d",&n,&m);
for(i=0;i<m;i++)
{
scanf("%d %d",&x,&y);
a[x]++; //把出现的数对作为数组a的下标,记录存在
a[y]++;
}
for(i=1;i<=n;i++)
{
if(a[i]<1) //寻找那个公共点cnt
{
cnt=i;
break;
}
}
printf("%d
",n-1);
for(i=1;i<=n;i++)
{
if(i!=cnt)
{
printf("%d %d
",i,cnt); //依次输出与公共点相连的点
}
}
return 0;
}
//https://blog.csdn.net/coco_astrids/article/details/52592418