787. 归并排序

题目描述

给定你一个长度为n的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式

输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在1~109范围内），表示整个数列。

输出格式

输出共一行，包含 n 个整数，表示排好序的数列。

数据范围

1≤n≤100000

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

算法描述

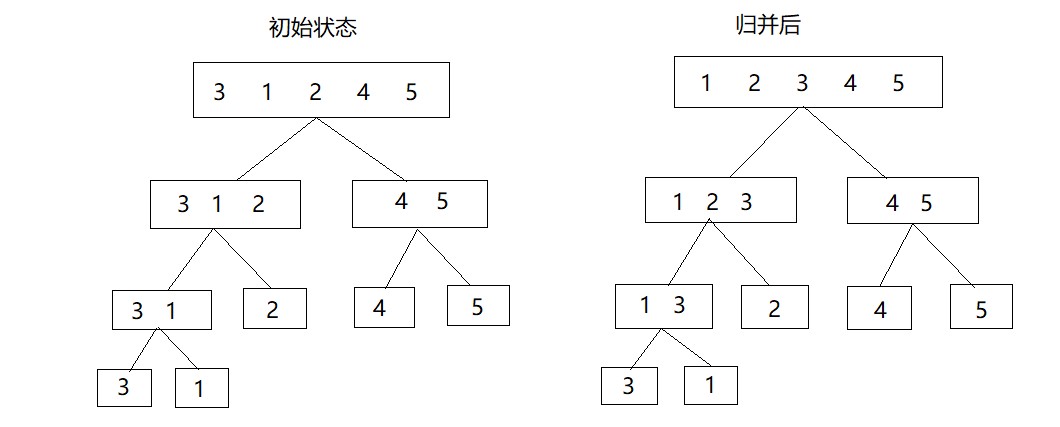
归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法采用分治法.

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并操作的工作原理如下：

第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列

第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置

第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置

重复步骤3直到某一指针超出序列尾

将另一序列剩下的所有元素直接复制到合并序列尾

（以上算法描述来自百度百科）

#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;
const int max_n=1e5+5;

int a[max_n], b[max_n];

void mergeSort(int l, int r) {
    if(l>=r) return;
    int mid=l+r >> 1;
    mergeSort(l, mid);
    mergeSort(mid+1, r);
    int p1=l, p2=mid+1, cnt=l;
    while(p1<=mid && p2<=r) {
        if(a[p1]<=a[p2]) b[cnt++]=a[p1++];
        else b[cnt++]=a[p2++];
    }
    while(p1<=mid) b[cnt++]=a[p1++];
    while(p2<=r) b[cnt++]=a[p2++];
    for(int i=l; i<=r; i++) 
        a[i]=b[i];
}

int main() {
    int n;
    cin>>n;
    for(int i=0; i<n; i++) cin>>a[i];
    mergeSort(0, n-1);
    for(int i=0; i<n; i++) cout<<a[i]<<' ';
    return 0;
}