1. 原理
仿射变换(Affine Transformation 或Affine Map)是一种二维坐标(x, y)到二维坐标(u, v)的线性变换,其数学表达式形式如下:
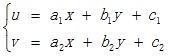
对应的齐次坐标矩阵表示形式为:
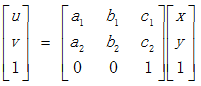
仿射变换保持了二维图形的“平直性”(直线经仿射变换后依然为直线)和“平行性”(直线之间的相对位置关系保持不变,平行线经仿射变换后依然为平行线,且直线上点的位置顺序不会发生变化)。非共线的三对对应点确定一个唯一的仿射变换。
2. 二维图像仿射变换
图像处理中,可应用仿射变换对二维图像进行平移、缩放、旋转等操作。实例如下:
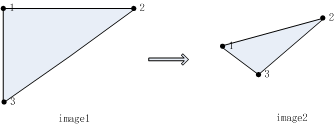
经仿射变换后,图像关键点依然构成三角形,但三角形形状已经发生变化。
3. 原子变换
仿射变换通过一系列原子变换复合实现,具体包括:平移(Translation)、缩放(Scale)、旋转(Rotation)、翻转(Flip)和错切(Shear)。
a. 平移
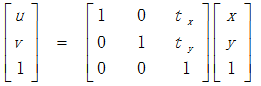
b. 缩放

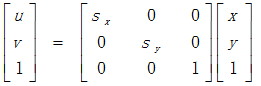
c. 旋转
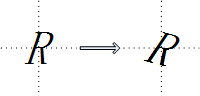

d. 翻转
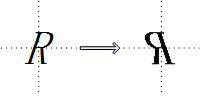
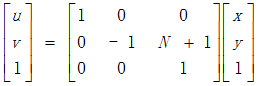
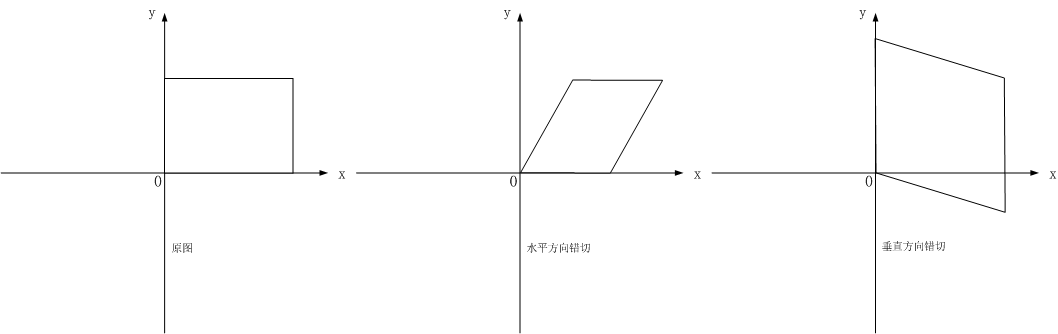
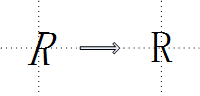
e. 错切
错切亦称为剪切或错位变换,包含水平错切和垂直错切,常用于产生弹性物体的变形处理。
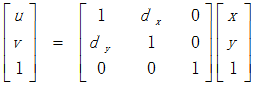
4. 程序
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
clc;clear all;close all;clc;image = imread('jyy.png');% u = 4 * x and v = 2 * yT = [4 0 0; 0 2 0; 0 0 1];% create spatial transformation structure.transformation = maketform('affine', T);% apply 2D spatial transformation to image.transformationResult = imtransform(image, transformation); |
结果示例:

