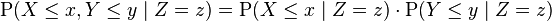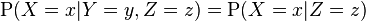文章作者：程欣宇 http://angeleyes.diandian.com/?p=244
这个例子很好理解，A是熬夜，C是懒床，B是迟到。一般情况下，熬夜会增加懒床的概率，懒床会增加迟到的概率。当然，天气冷也会增加懒床的概率，堵车也会增加迟到的概率，现实生活中的可能性是很多的，我们现在只关注A熬夜和B迟到的概率P(A)、P(B)之间的关系。
显然，熬夜发生的情况下，迟到的概率是增加的。但有一种情况例外：就是已经知道今天已经懒床了，同时不知道是否熬夜了，也不知道是否会迟到，这时候，熬夜和迟到发生的概率就无关了。因为懒床已经确定（不管是因为熬夜、天气冷、工作轻松或者是其它任何原因产生的）的情况下，懒床导致的迟到可能性也确定了，熬夜已经不可能通过增加懒床的概率来间接增加迟到的概率了，那么迟到的概率和和熬夜的概率也就没有依赖关系了，记为：熬夜 ╨ 迟到 | 懒床。
这种本来不是独立的随机事件，在满足一定条件下，他们独立了，这就叫有条件的独立，简称条件独立，可以帮助化简不少概率计算，在模式识别中也很有用。
Definition：if A ╨ B|C (meaning A is independent of B given C) means that given evidence at C, A is independent of B。
除了上面熬夜到迟到的例子，我们也可以用最直观的文氏图来说明这种情况：
首先，我们把全体Ｉ分为Ａ和非Ａ两部分
然后，我们引入Ｃ，从下图可以看出，Ａ中Ｃ的比例要高于非Ａ中Ｃ的比例，所以Ａ和Ｃ相关
最后，我们引入Ｂ，从下图可以看出，Ｃ中Ｂ的比例要高于非Ｃ中Ｂ的比例，所以Ｃ和Ｂ相关，但是，对于Ｃ中的Ａ和Ｂ的情况，可以看出无论Ａ发生与否，Ｂ都是大约2/3的概率，对于非C中的A和B的情况来看，无论A发生与否，B都是大约1/2的概率，也就是说，一旦C确定，B的概率就确定了，和A无关。
定义：http://zh.wikipedia.org/wiki/%E7%B5%B1%E8%A8%88%E7%8D%A8%E7%AB%8B%E6%80%A7
直觉地，两个随机变量X和Y给定Z条件独立，如果：一旦知道了Z，从Y的值便不能得出任何关于X的信息。例如，相同的数量Z的两个测量X和Y不是独立的，但它们是给定Z条件独立（除非两个测量的误差是有关联的）。
条件独立的正式定义是基于条件分布的想法。如果X、Y和Z是离散型随机变量，那么我们定义X和Y给定Z条件独立，如果对于所有使
的x、y和z，都有：
另一方面，如果随机变量是连续的，且具有联合概率密度p，那么X和Y给定Z条件独立，如果对于所有使
的实数x、y和z，都有：
如果X和Y给定Z条件独立，那么对于任何满足
的x、y和z，都有：
也就是说，X给定Y和Z的条件分布，与仅仅给定Z的条件分布是相同的。对于连续的情况下的条件概率密度函数，也有一个类似的公式。
独立性可以视为条件独立的一个特例，因为概率可以视为不给定任何事件的条件概率。