归并排序
归并排序,顾名思义,就是通过将两个有序的序列合并为一个大的有序的序列的方式来实现排序。合并排序是一种典型的分治算法:首先将序列分为两部分,然后对每一部分进行循环递归的排序,然后逐个将结果进行合并。

归并排序的时间复杂度为O(nlgn),这个是我们之前的选择排序和插入排序所达不到的。它是一种稳定性排序,也就是相等的元素在序列中的相对位置在排序前后不会发生变化。他的唯一缺点是,需要利用额外的N的空间来进行排序。
原理

合并排序依赖于合并操作,即将两个已经排序的序列合并成一个序列,具体的过程如下:
- 申请空间,使其大小为两个已经排序序列之和,然后将待排序数组复制到该数组中。
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较复制数组中两个指针所指向的元素,选择相对小的元素放入到原始待排序数组中,并移动指针到下一位置
- 重复步骤3直到某一指针达到序列尾
- 将另一序列剩下的所有元素直接复制到原始数组末尾
该过程实现如下,注释比较清楚:
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
for (int k = lo; k <= hi; k++) {
aux[k] = a[k];
}
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
下图是使用以上方法将EEGMR和ACERT这两个有序序列合并为一个大的序列的过程演示:

实现
合并排序有两种实现,一种是至上而下(Top-Down)合并,一种是至下而上 (Bottom-Up)合并,两者算法思想差不多,这里仅介绍至上而下的合并排序。至上而下的合并是一种典型的分治算法(Divide-and-Conquer),如果两个序列已经排好序了,那么采用合并算法,将这两个序列合并为一个大的序列也就是对大的序列进行了排序。
首先我们将待排序的元素均分为左右两个序列,然后分别对其进去排序,然后对这个排好序的序列进行合并,代码如下:
public class Merge {
private Merge() { }
// stably merge a[lo .. mid] with a[mid+1 ..hi] using aux[lo .. hi]
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
for (int k = lo; k <= hi; k++) {
aux[k] = a[k];
}
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort(a, aux, lo, mid);
sort(a, aux, mid + 1, hi);
merge(a, aux, lo, mid, hi);
}
public static void sort(Comparable[] a) {
Comparable[] aux = new Comparable[a.length];
sort(a, aux, 0, a.length-1);
assert isSorted(a);
}
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
}
以排序一个具有15个元素的数组为例,其调用堆栈为:

我们单独将Merge步骤拿出来,可以看到合并的过程如下:

图示及动画
如果以排序38,27,43,3,9,82,10为例,将合并排序画出来的话,可以看到如下图:

下图是合并排序的可视化效果图:

对6 5 3 1 8 7 24 进行合并排序的动画效果如下:

下图演示了合并排序在不同的情况下的效率:

改进
对合并排序进行一些改进可以提高合并排序的效率。
1. 当划分到较小的子序列时,通常可以使用插入排序替代合并排序
对于较小的子序列(通常序列元素个数为7个左右),我们就可以采用插入排序直接进行排序而不用继续递归了),算法改造如下:
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
if (hi-lo+1<阈值) selectionSort(a);
sort(a, aux, lo, mid);
sort(a, aux, mid + 1, hi);
merge(a, aux, lo, mid, hi);
}
2. 如果已经排好序了就不用合并了
当已排好序的左侧的序列的最大值<=右侧序列的最小值的时候,表示整个序列已经排好序了。

算法改动如下:
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
if (hi-o+1<阈值) selectionSort(a);
sort(a, aux, lo, mid);
sort(a, aux, mid + 1, hi);
if(a[mid]<a[mid+1])return;
merge(a, aux, lo, mid, hi);
}
3. 并行化
分治算法通常比较容易进行并行化,在浅谈并发与并行这篇文章中已经展示了如何对快速排序进行并行化(快速排序在下一篇文章中讲解),合并排序一样,因为我们均分的左右两侧的序列是独立的,所以可以进行并行,值得注意的是,并行化也有一个阈值,当序列长度小于某个阈值的时候,停止并行化能够提高效率,这些详细的讨论在浅谈并发与并行这篇文章中有详细的介绍了,这里不再赘述。
自底向上的归并排序

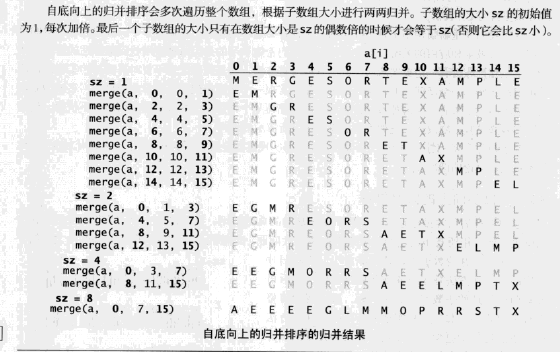
代码实现
public class MergeBU {
private MergeBU() { }
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
for (int k = lo; k <= hi; k++) {
aux[k] = a[k];
}
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
public static void sort(Comparable[] a) {
int N = a.length;
Comparable[] aux = new Comparable[N];
for (int n = 1; n < N; n = n+n) {
for (int i = 0; i < N-n; i += n+n) {
int lo = i;
int m = i+n-1;
int hi = Math.min(i+n+n-1, N-1);
merge(a, aux, lo, m, hi);
}
}
}
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
}
用途
合并排序和快速排序一样都是时间复杂度为nlgn的算法,但是和快速排序相比,合并排序是一种稳定性排序,也就是说排序关键字相等的两个元素在整个序列排序的前后,相对位置不会发生变化,这一特性使得合并排序是稳定性排序中效率最高的一个。在Java中对引用对象进行排序.