本节是cs231学习笔记:最优化,并介绍了梯度下降方法,然后应用到逻辑回归中
引言
在上一节线性分类器中提到,分类方法主要有两部分组成:1.基于参数的评分函数。能够将样本映射到类别的分值。2.损失函数。用来衡量预测标签和真是标签的一致性程度。这一节介绍第三个重要部分:最优化(optimization)。损失函数能让我们定量的评估得到的权重W的好坏,而最优化的目标就是找到一个W,使得损失函数最小。工作流程如下图:
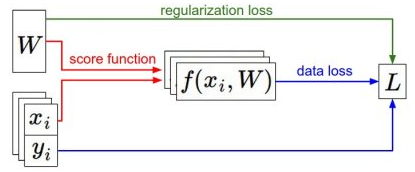
(x,y)是给定的数据集,W是权重矩阵,通过初始化得到。向前传递到评分函数中得到类别的评分值并存储在向量f中。损失函数计算评分函数值f与类标签y的差值,正则化损失只是一个关于权重的函数。在梯度下降过程中,我们计算权重的梯度,然后使用梯度更新权重。一旦理解了这三个部分的关系,我们可以用更加复杂的评分函数来代替线性映射,比如神经网络、甚至卷积神经网络等,而损失函数和优化过程这两部分则相对保持不变。
梯度下降
梯度下降的思想是:要寻找某函数的最值,最好的方法就是沿着函数的梯度方向寻找,移动量的大小称为步长。梯度下降的公式如下:
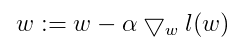
我们常常听说过梯度上升、梯度下降,那么两者的区别又是什么呢?其实这两者是一样的,只是公式中的减法变成加法,因此公式为:
![]()
梯度上升是用来求函数的最大值,而梯度下降是用来求最小值。普通的梯度下降版本如下:
# 普通的梯度下降 while True: weights_grad = evaluate_gradient(loss_fun, data, weights) weights += - step_size * weights_grad # 进行梯度更新
其中的evaluate_gradient是用来计算梯度的,data是训练样本集,weights是权重,step_size是下降的步长。梯度下降方法对神经网络的损失函数优化中最常用的方法,核心思想就是一直沿着梯度方向走,直到结果不变为止。梯度下降每次更新权重W时都需要遍历整个数据集,当训练数据达到百万级别的时候,上面的方法将会十分的耗时,一种改进的方法是:
小批量数据梯度下降(Mini-batch gradient descent):这种方法一次仅用一个或一部分数据来更新权重,例如在目前最先进的卷及神经网络中,训练集有一百而是多万,一个小批量中包含256个样本。小批量梯度下降的版本:
# 普通的小批量数据梯度下降 while True: data_batch = sample_training_data(data, 256) # 256个数据 weights_grad = evaluate_gradient(loss_fun, data_batch, weights) weights += - step_size * weights_grad # 参数更新
这种方法之所以效果不错,是因为训练集中存在相关的样本。要理解这一点,可以想想一种极端情况,在ILSVRC中,120W个图像是1000张不同的图片,每张复制1200份得到,对比这120W张图片的损失均值应该和这1000张子集损失值一样。实际数据集中,不会包含这么多重复图像,所以小批量梯度下降方法是对整个数据集梯度的一个近似。因此小批量梯度下降方法能够更快的收敛,并更加频繁的更新参数。
小批量数据梯度下降方法有一个极端情况,那就是小批量中只有1个数据样本,这种方法被称作随机梯度下降(SGD,Stochastic Gradient Descent)或者被成为在线(on-line)梯度下降,这种方法在实际操作中使用的并不多,因为使用向量化的代码计算包含100个样本的梯度效率要比计算100次1个样本梯度的效率高的多。但SGD常常被用来指代MGD,或者当看到“使用SGD”,我们就假定使用的是MGD。小批量数据集的大小是一个超参数,但是不需要通过交叉验证来调参,依赖存储器的大小。
实例
下面引用《机器学习实战》中对logistics regression求参数的例子来帮助理解梯度优化算法,下面是梯度上升代码:
def gradAscent(raw_data,label): #转化为矩阵类型 train_X = np.mat(raw_data) train_Y = np.mat(label).T m,n = train_X.shape weights = np.ones((n,1)) alpha = 0.001 for i in xrange(500): h = sigmoid(train_X * weights) error = (train_Y - h) weights += alpha*train_X.T*error return weights
其中for循环是整个数据集的迭代次数,weights是一个向量,长度为数据集维度的个数。需要注意的是h、error是一个列向量,元素的个数为数据集的大小。其中weights += alpha*train_X.T*error为逻辑回归损失函数梯度迭代公式。可以看出每次迭代都需要对整个数据集进行计算。下面给出随机梯度上升的代码,一次仅用一个样本来更新权重。
def stocGradAscent(train_X,train_Y): train_X = np.array(train_X) m,n = train_X.shape alpha = 0.01 weights = np.ones(n) for i in range(m): h = sigmoid(sum(train_X[i] * weights)) error = int(train_Y[i]) - h weights += alpha * error * train_X[i] return weights
与上面的代码不同的是,for循环迭代的次数是数据集的大小,每次选取一个样本用来更新权重,其中的h和error不再是向量而是一个数值。
上面两个方法使用的学习率为0.01,学习率代表算法学习速度的快慢。学习率、迭代次数与损失函数的关系如下图:
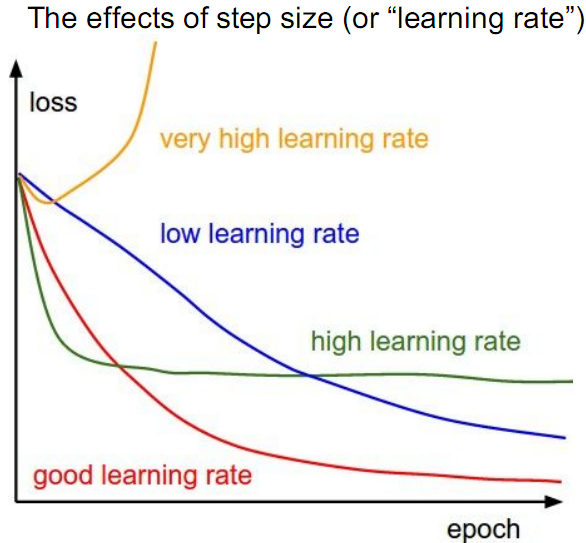
除了梯度下降(上升)算法之外,还有一些最小化损失函数的算法,这些算法更加的复杂和优越,通常也不需要人工选择学习率例如:共轭梯度(Conjugate Gradient)、局部优化法(Broyden Fletcher goldfard shann,BFGS)等等,这些方法等遇到了再来补充,有兴趣的可以自行查阅资料。(完)