二叉树
一、树的概念
1、设某二叉树中度数为 0 的结点数为 N0,度数为 1 的结点数为 Nl,度数 为 2 的结点数为 N2,则下列等式成立的是 N0=N2+1(图解示例)

二、二叉树
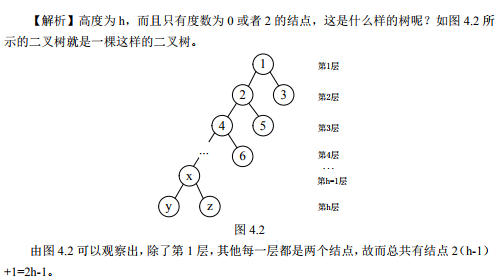
1、设高度为h的二叉树上只有度为0和度为2的结点,则此类二叉树中包含的结点数至少是多少(图解示例)
2、尽管二叉树和树有许多相似之处,但是二叉树不是树的特殊情况
3、
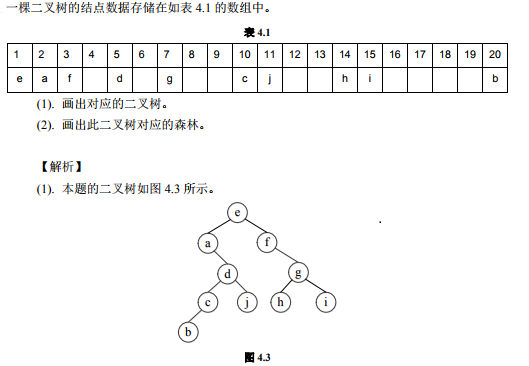
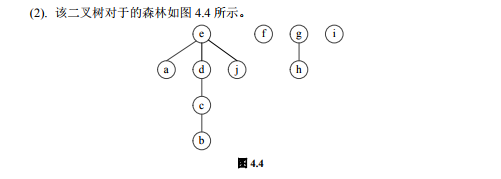
三、二叉树的遍历
1、先序序列和中序序列,中序序列和后序序列可以确定一棵二叉树
2、
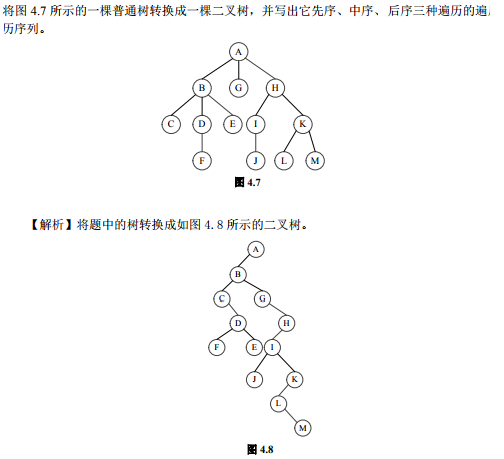
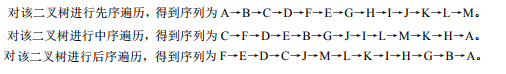
3、
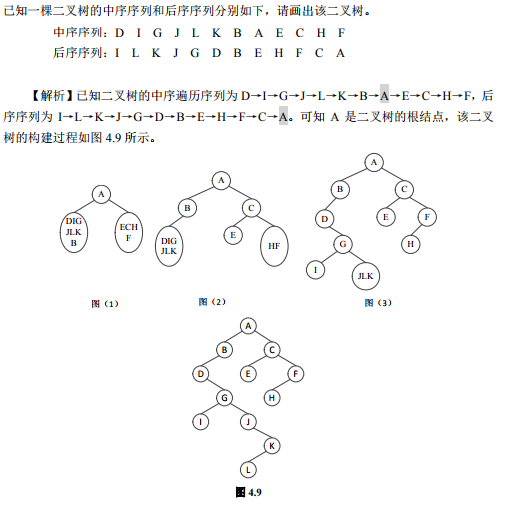
四、树与森林
1、

2、将图 4.13 所示的树转换成二叉树,并写出该二叉树的先序遍历序列。

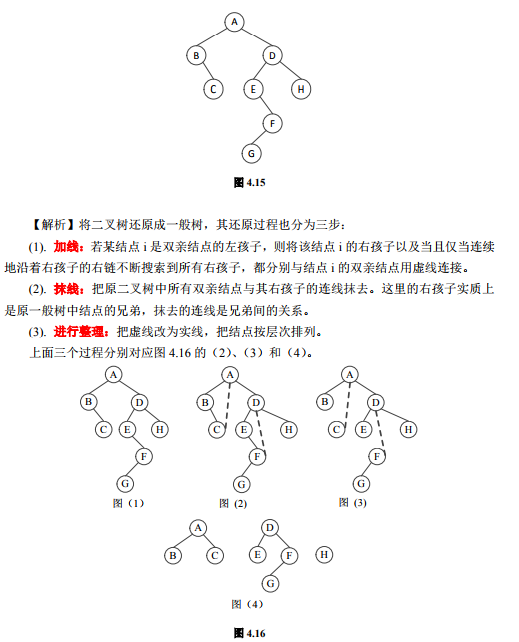
3、已知某森林的二叉树如图 4.15 所示,试画出它所表示的森林。
五、树与二叉树的应用
一、二叉排序树
1、设二叉排序树上有n个结点,则在二叉排序树上查找结点的平均时间复杂度为——O(log2N)
2、在二叉排序树中插入一个结点的平均时间复杂度——O(log2N)
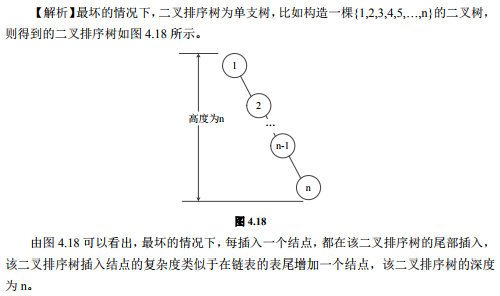
3、若构造一棵具有n个结点的二叉排序树,最坏的情况其深度不超过——n(图解示例)
4、
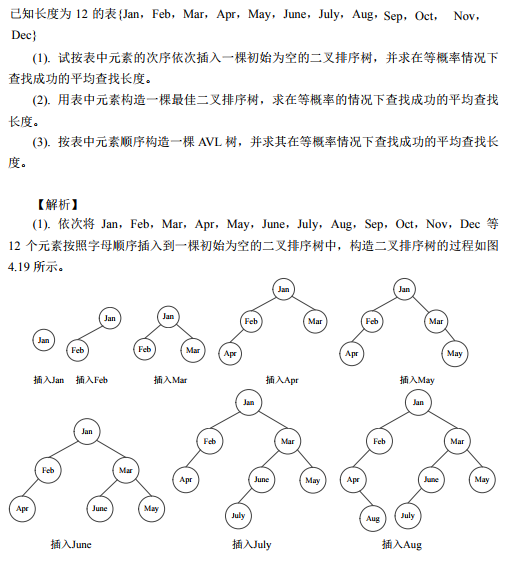
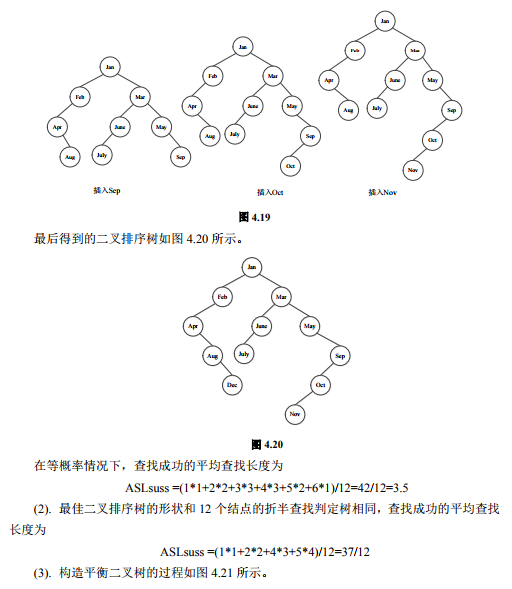
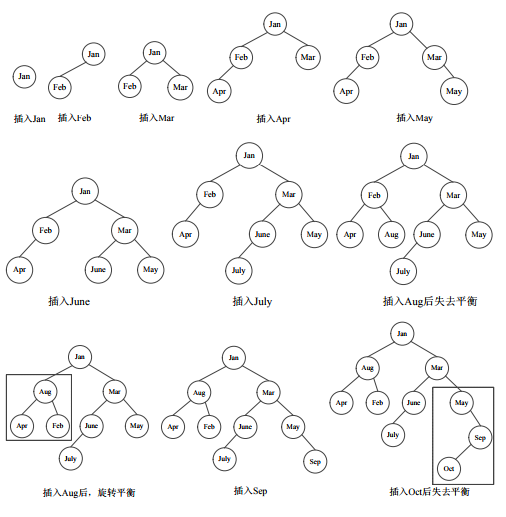
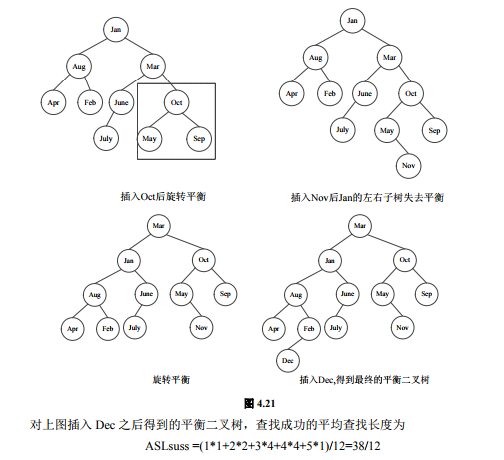
二、平衡二叉树
1、)设关键字的输入序列为{4,5,7,2,1,3,6}
(1). 从空树开始构造平衡二叉树,画出每加入一个新结点时二叉树的形态,若发生不 平衡,指明需做的平衡旋转类型及平衡旋转的结果。
(2). 上面的数据作为待排序的数据,写出用快速排序进行一趟划分后的数据序列。
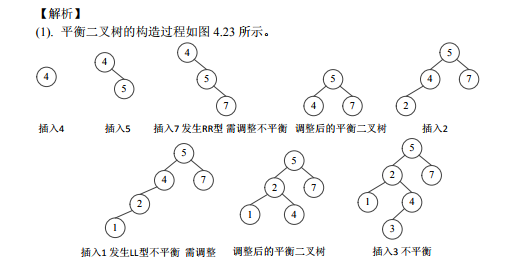
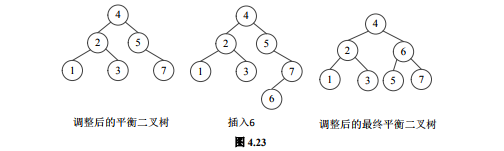
(2)一趟划分后的数据序列为 3、1、2、4、7、5、6。
三、哈夫曼树和哈夫曼编码
1、有n个叶子的哈夫曼树的结点总数——2n-1
2、设某哈夫曼树中有199个结点,则该哈夫曼树中有多少个叶子结点(图解示例)

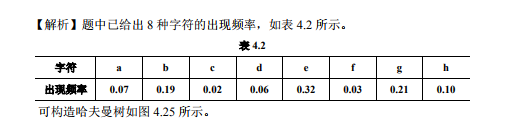
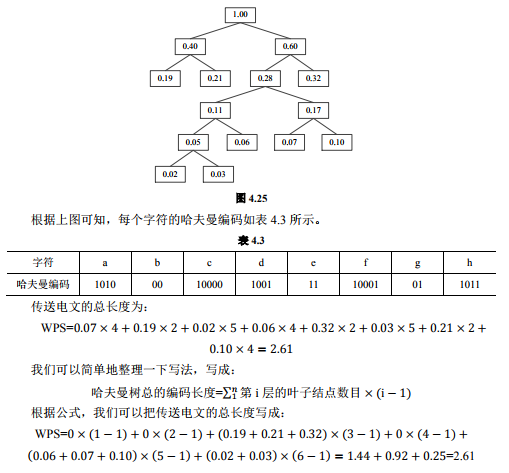
3、在一份电文中共使用 8 种字符,即 a, b, c, d, e, f, g, h,它们出现的频率 依次为 0.07, 0.19,0.02,0.06, 0.32, 0.03, 0.21, 0.10,
试画出对应的哈夫曼树,求出每个字 符的哈夫曼编码,并求出传送电文的总长度。