题意
有一个(n imes m)的矩阵。机器人从点((x,y))开始等概率的往下,往右,往左走或者不动。如果再第一列,那么不会往左走,再第m列不会往右走。也就是说机器人不会走出这个格子。走到最后一行会停止。求出机器人期望行走的步数。
思路
设(f[i][j])表示从((i,j))走到最后一行的期望步数。
显然最后一行的答案为0
然后考虑其他行。假设(j!=m)并且(j!=1)那么有
[f[i][j]=1+frac{1}{4}(f[i][j+1]+f[i][j-1]+f[i][j]+f[i+1][j])
]
然后这个(dp)具有后效性,无法直接转移
通分移项可得
[f[i + 1][j] + 4 = 3f[i][j] - f[i][j - 1] - f[i][j + 1]
]
这样对于每一行我们就可以列出来一个(m)元的方程组。
然后发现(f)数组的每一行都可以用一次高斯消元解出来。
(j=1)或者(j=m)??
和上面一样的思路,稍微改一下(dp)方程即可
如下
[f[1][j] + 3=2f[1][j] - f[1][j+1]
]
[f[m][j] + 3=2f[m][j] - f[m][j-1]
]
复杂度???
因为这个高斯消元的矩阵列出来是一个这样的矩阵
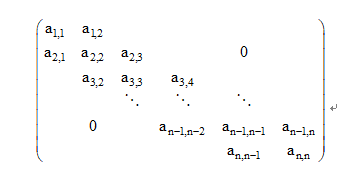
所以其实是可以(O(m))的解的。
所以总复杂度是(O(nm))
代码
这是一份取模版(模数为(998244353))的代码,直接交到(CF)上会(WA)!!!
/*
* @Author: wxyww
* @Date: 2019-03-16 08:00:47
* @Last Modified time: 2019-03-16 16:20:43
*/
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#include<ctime>
using namespace std;
typedef long long ll;
const int mod = 998244353,N = 1010;
#define int ll
ll read() {
ll x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9') {
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
int Bx,By,n,m,f[N][N],g[N][N];
ll qm(ll x,ll y) {
ll ans = 1;
for(;y;y >>= 1,x = x * x % mod)
if(y & 1) ans = ans * x % mod;
return ans;
}
void solve(int x) {
g[1][m + 1] = f[x + 1][1] + 3;
g[m][m + 1] = f[x + 1][m] + 3;
for(int i = 2;i < m;++i) g[i][m + 1] = f[x + 1][i] + 4;
f[x][1] = g[1][1];f[x][2] = g[1][2];f[x][m + 1] = g[1][m + 1];
for(int i = 2;i <= m;++i) {
int k1 = f[x][i - 1],k2 = g[i][i - 1];
f[x][i - 1] = (1ll * f[x][i - 1] * k2 % mod - (1ll * g[i][i - 1] * k1 % mod) + mod) % mod;
f[x][i] = (1ll * f[x][i] * k2 % mod - (1ll * g[i][i] * k1 % mod) + mod)% mod;
if(i != m)
f[x][i + 1] = (1ll * f[x][i + 1] * k2 % mod - (1ll * g[i][i + 1] * k1 % mod) + mod) % mod;
f[x][m + 1] = (1ll * f[x][m + 1] * k2 % mod - (1ll * g[i][m + 1] * k1 % mod) + mod) % mod;
}
f[x][m] = 1ll * f[x][m + 1] * qm(f[x][m],mod - 2) % mod;
f[x][m - 1] = 1ll * (g[m][m + 1] - (1ll * g[m][m] * f[x][m] % mod) + mod) % mod * qm(g[m][m - 1],mod - 2) % mod;
for(int i = m - 1;i > 1;--i)
f[x][i - 1] = ((g[i][m + 1] - ((f[x][i] * g[i][i] % mod + mod)% mod) - (f[x][i + 1] * g[i][i + 1] % mod)) % mod + mod) % mod * qm(g[i][i - 1],mod - 2) % mod;
}
signed main() {
n = read(),m = read();
Bx = read(),By = read();
if(m == 1) {printf("%lld
",2ll * (n - Bx) % mod); return 0;}
g[1][1] = 2;g[1][2] = mod - 1;
g[m][m - 1] = mod - 1,g[m][m] = 2;
for(int i = 2;i < m;++i)
g[i][i] = 3,g[i][i + 1] = mod - 1,g[i][i - 1] = mod - 1;
for(int i = n - 1;i >= Bx;--i) solve(i);
cout<<f[Bx][By];
return 0;
}