此文章已于 16:41:13 2013/4/26 重新发布到 wybang
更加全面地认识PCA
类别 机器学习, 数据挖掘
相信只要与数据打交道的同学对PCA都不陌生,不管是机器学习/数据挖掘的同仁,还是从事图像处理、信号分析的研究者。PCA有着十分广泛的应用,常见的应用有降维(dimensionality reduction)、特征提取(feature extraction)、有损数据压缩(lossy data compression)、去噪(denoising)等。但我们真的认识PCA吗?不少同学学习PCA的时候都是从最大化方差的优化角度来认识她的,她真如某句话说的那样"美女只会美一面"吗?下面我们一起从多个角度重新来审视这个仙女。这里,我们并不先对PCA做一种先验的定义,而是先来看几个问题。通过对这些问题最后形式的统一来解释什么是PCA。
(一)最大化方差(Maximum variance )
考虑如下一个问题:假设我手边现在有一堆观测数据{Xn}n=1,2,…,N,其中Xn∈RD,但是根据我对数据的观察,发现Xn中有部分维数之间的线性相关性表现十分明显,所以我希望把数据投影到一个更加低维的空间RM下(其中M是给定的),但是希望数据中的信息尽可能地保留。但如何衡量数据中的信息呢?信息量很多时候可以用差异度这个概念去量化,比如熵的定义中也有这样的影子。这里选择方差(variance)来衡量信息量。
考虑M=1的情况,假设此时的投影向量为u1,均值 ,那么投影后数据的方差为
,那么投影后数据的方差为 ,现在我们的目的是要最大化Obj目标,求un。需要注意的是,由于u1没有尺度的限制,可能有多个解,为了便于求解,需要添加一个normalization约束。综上,优化问题如下:
,现在我们的目的是要最大化Obj目标,求un。需要注意的是,由于u1没有尺度的限制,可能有多个解,为了便于求解,需要添加一个normalization约束。综上,优化问题如下: ,
,
根据拉格朗日乘子法, ,对u1求偏导,得
,对u1求偏导,得 。即u1是S的特征向量,不难发现
。即u1是S的特征向量,不难发现 ,即最大方差就是S最大特征向量。
,即最大方差就是S最大特征向量。
将此结论推广到M>1的情况下,即投影向量为S的前M个最大特征值对应的特征向量,最大方差为这前M个最大特征值之和。
(二)最小化残差(Minimum error)
还是针对上面的数据,假设在原始空间RD的一组正交基为{ ui}。对于原数据任意Xn的都有可以用其所在空间的正交基线性表示为: ,现在我们希望用一个数量比D小的M个线性无关向量来近似{X},希望
,现在我们希望用一个数量比D小的M个线性无关向量来近似{X},希望 。最优化目标函数如下:
。最优化目标函数如下: 。分别对zni和bi求偏导并令其等于0,得如下,
。分别对zni和bi求偏导并令其等于0,得如下,


根据{ ui}的正交性,不难得出, 。将上述等式带入J中,得
。将上述等式带入J中,得 ,优化问题如下:
,优化问题如下:
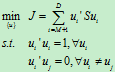
同样可以根据拉格朗日乘子法,得到 ,
, 。
。
从上面两个问题中可以看到,想要经过投影使得在新空间下数据的方差最大和想要通过更"少"的无关向量来近似原数据都和协方差矩阵S的特征向量和特征值有关。现在来解释PCA。Principal component analysis中什么是Principal component?其实就是S中最大特征值对应的特征向量。