21:56:35 在你眼中我是谁,你想我代替谁。——廖俊涛《谁》
害,这个题目一出来的时候就傻眼了。
好了,现在让我们来看一下这些神仙题目。
第一题:电路图a
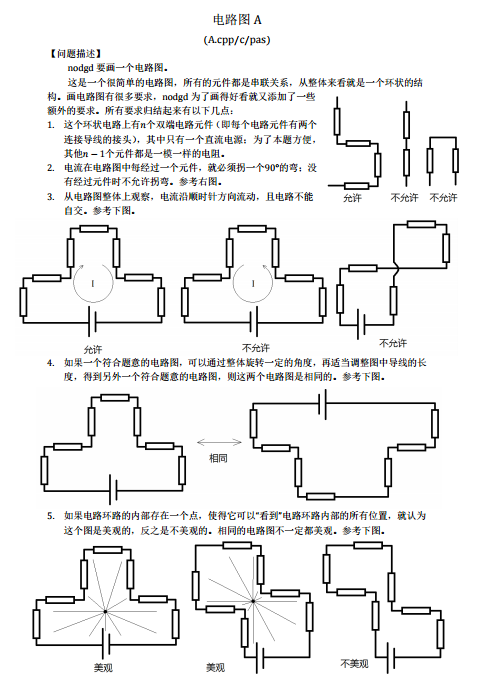
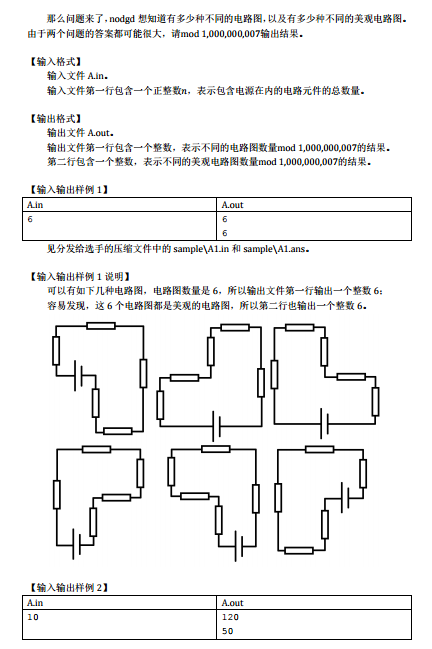
首先由于题目中说每两个元件之间必须拐90度,因此电路图可以表示为一个长度为n的L和R组成的序列,其中L代表一个左拐,R代表一个右拐
因为电路图最后要拐360度回到起点,所以L和R的数量l,r有这么一个关系: l = r-4
然后就变成了不同排列的序列个数问题,转换成计算n中选(n-4)/2个元素的组合数,组合数公式:Cmn=n!/(m!(n-m)!)
算组合数+取模运算为了应对有个小技巧,模除法需要转换为乘逆元.也可以用logp的费马小定理(a*a^(p-2) 同余 1 (mod p) ,所以a^(p-2)为a逆元,用快速幂log p求得
又因为这个图转化为的序列是首尾相接的环,所以位置1和位置n不能同为L,分类讨论之后可以得到这个答案等于组合数之差
#include<bits/stdc++.h> using namespace std; typedef long long ll; const ll mod=1000000007; ll sby(ll a,ll b){ ll o=1; while(b){ if(b&1) o*=a,o%=mod; a*=a,a%=mod; b>>=1; } return o; } ll ss(ll a,ll b){ ll c1=1,c2=1; for(int i=a+1;i<=b;i++) c1*=i,c1%=mod; for(int i=b-a;i;i--) c2*=i,c2%=mod; return (c1*sby(c2,mod-2))%mod; } int main(){ int n; scanf("%d",&n); ll k=(n-4)/2,p=ss((n+4)/2,n); ll ans2=(2ll*ss(k,n-k)%mod-ss(k,n-k-1))%mod; if(ans2<0) ans2+=mod; printf("%lld ",p); printf("%lld ",ans2); return 0; }
第二题:电路图b

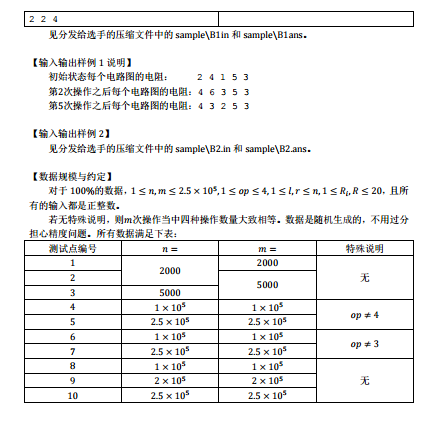
首先回忆一下初中物理知识,
两个电阻R1,R2 ;
并联的后的电阻R1∗R2/(R1+R2)
考虑如何实现这个线段树标记,
如果是串联,就是直接加,非常方便。
但是标记要合并,要将两种标记实现合并,
设一个标记为(a,b,c,d)一个四元组。
表示x在这个标记之下变为了x∗(ax+b)/(cx+d)
于是就可以发现这个标记可以合并。
这道题在当时没有打出来,因为真的太难太难了。
#include<bits/stdc++.h> #define fo(i,a,b) for(int i=a;i<=b;++i) #define fd(i,a,b) for(int i=a;i>=b;--i) using namespace std; const int N=25e4+5; const long double nn=1e9,mm=0; int n,m,oo,pp,qq,aa,e[N]; long double ans; struct sby { long double a,b,c,d,mx,mn; }xz[4*N]; void clear(int x)//初始化,可不是全都是0哦~ { xz[x].a=xz[x].d=1,xz[x].b=xz[x].c=0; } void mix(sby &p,sby q)//合并标记 { p.mx=(q.a*p.mx+q.b)/(q.c*p.mx+q.d); p.mn=(q.a*p.mn+q.b)/(q.c*p.mn+q.d); long double a=q.a*p.a+q.b*p.c,b=q.a*p.b+q.b*p.d; long double c=q.c*p.a+q.d*p.c,d=q.c*p.b+q.d*p.d; p=(sby){1,b/a,c/a,d/a,p.mx,p.mn}; } void down(int x) { mix(xz[x<<1],xz[x]); mix(xz[x<<1|1],xz[x]); clear(x); } void ss(int x) { xz[x].mn=min(xz[x<<1].mn,xz[x<<1|1].mn); xz[x].mx=max(xz[x<<1].mx,xz[x<<1|1].mx); } void build(int x,int l,int r) { clear(x); if(l==r) { xz[x].mx=xz[x].mn=e[l]; return; } int mid=(l+r)>>1; build(x<<1,l,mid); build(x<<1|1,mid+1,r); ss(x); } long double get(long double v) { return v*aa/(v+aa); } void calc(int x,int l,int r) { if(l^r) down(x); if(pp<=l&&qq>=r) { if(oo==1) ans=max(ans,xz[x].mx); if(oo==2) ans=min(ans,xz[x].mn); if(oo==3) xz[x]=(sby){1,aa,0,1,xz[x].mx+aa,xz[x].mn+aa}; if(oo==4) xz[x]=(sby){aa,0,1,aa,get(xz[x].mx),get(xz[x].mn)}; return; } int mid=(l+r)>>1; if(pp<=mid) calc(x<<1,l,mid); if(qq>mid) calc(x<<1|1,mid+1,r); if(oo>=3) ss(x); } int main() { scanf("%d",&n); fo(i,1,n) scanf("%d",&e[i]); build(1,1,n); scanf("%d",&m); fo(i,1,m) { scanf("%d%d%d",&oo,&pp,&qq); if(oo<=2) { if(oo==1) ans=mm; else ans=nn; calc(1,1,n); printf("%.10lf ",(double)ans); } else scanf("%d",&aa),calc(1,1,n); } return 0; }
第三题:电路图c

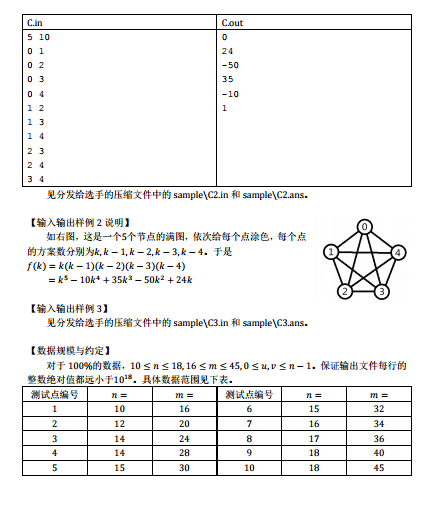
这道题就放这了,等待某位大佬来解答!!!我很抱歉没有做出这道题!!!