题目描述
在放完棋子之后,$dirty$又开始了新的游戏。
现在他拥有一个长为$n$的数组$A$,他定义第$i$个位置的分值为$i−k+1$,其中$k$需要满足:
对于任意满足$kleqslant jleqslant i$的$j$,有$A[k]leqslant A[j]leqslant A[i]$。当对于第$i$个数,有多个$k$满足条件时,取能获得较大分值的$k$。
现在,$dirty$想要知道$A$数组中分值最大的位置对应的分值为多少。
输入格式
第一行一个整数$n$,表示$A$数组的长度。
第二行$n$个整数,第$i$个数表示$A[i]$的值。
输出格式
输出一行一个整数,表示$A$数组中分值最大的位置对应的分值。
样例
样例输入:
8
8 6 1 7 9 2 3 8
样例输出:
3
数据范围与提示
注意由于$n$的范围较大,本题可能需要使用更快的读入方法。
对于$10\%$的数据,$nleqslant 10^3$;
对于$40\%$的数据,$nleqslant 3 imes 10^5$;
对于另外$20\%$的数据为随机数据,且$nleqslant 10^6$;
对于$100\%$的数据,$1leqslant nleqslant 10^7$;$1leqslant A[i]leqslant 10^9$。
题解
先来解释一下题意,对于区间$[k,i]$,我们只用保证中间的所有元素都大于等于$A[k]$,比小于等于$A[i]$即可,而不用关注其内部大小关系。
分值越大意味着$k$越小。
接下来说一下我考场上的思路,发现对于每一个$i$其最小的$k$位于其前面最后一个比它大的数之间最小的数,也就是如下图$downarrow$
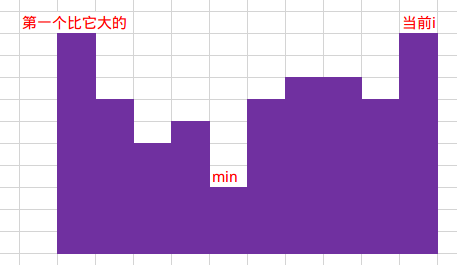
那么我们可以用单调栈维护第一个比它大的,然后用线段树查询区间最小值的位置即可,然后它就$downarrow$

这个思路最傻的地方在于为何不用单调栈在维护一个最小值……
时间复杂度:$Theta(n)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
$60\%$算法:
#include<bits/stdc++.h>
#define int int_least32_t
#define L(x) x<<1
#define R(x) x<<1|1
using namespace std;
const int L=1<<20|1;
char buffer[L],*S,*T;
#define inline __attribute__((optimize("-O3")))
#define getchar() ((S==T&&(T=(S=buffer)+fread(buffer,1,L,stdin),S==T))?EOF:*S++)
int n;
int a[10000010];
int ans;
int trmin[40000010],pmin[40000010];
int sta[10000010],top;
inline int read(){
int ss(0);char bb(getchar());
while(bb<48||bb>57)bb=getchar();
while(bb>=48&&bb<=57)ss=(ss<<1)+(ss<<3)+(bb^48),bb=getchar();
return ss;
}
inline void pushup(int x)
{
if(trmin[L(x)]<=trmin[R(x)])
{
trmin[x]=trmin[L(x)];
pmin[x]=pmin[L(x)];
}
else
{
trmin[x]=trmin[R(x)];
pmin[x]=pmin[R(x)];
}
}
inline void build(int x,int l,int r)
{
if(l==r){trmin[x]=a[l];pmin[x]=l;return;}
int mid=(l+r)>>1;
build(L(x),l,mid);
build(R(x),mid+1,r);
pushup(x);
}
inline pair<int,int> askmin(int x,int l,int r,int L,int R)
{
if(r<L||R<l)return make_pair(-0x3f3f3f3f,0x3f3f3f3f);
if(L<=l&&r<=R)return make_pair(pmin[x],trmin[x]);
int mid=(l+r)>>1;
pair<int,int> lft=askmin(L(x),l,mid,L,R);
pair<int,int> rht=askmin(R(x),mid+1,r,L,R);
return lft.second<=rht.second?lft:rht;
}
int main()
{
n=read();
for(int i=1;i<=n;i++)a[i]=read();
a[n+1]=0x3f3f3f3f;
build(1,1,n+1);
for(int i=1;i<=n;i++)
{
while(top&&a[sta[top]]<=a[i])top--;
int flag=sta[top]+1;
sta[++top]=i;
if(i-flag<ans)continue;
pair<int,int> minn=askmin(1,1,n+1,flag,i);
ans=max(ans,i-minn.first+1);
}
printf("%d",ans);
return 0;
}
$100\%$算法:
#include<bits/stdc++.h>
using namespace std;
int n;
int a[10000001],sta[10000001],maxn[10000001];
int ans;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
while(sta[0]&&a[i]<a[sta[sta[0]]])
{
if(a[maxn[sta[0]-1]]<=a[maxn[sta[0]]])maxn[sta[0]-1]=maxn[sta[0]];
ans=max(ans,maxn[sta[0]]-sta[sta[0]]+1);
maxn[sta[0]--]=0;
}
sta[++sta[0]]=i;
maxn[sta[0]]=i;
}
while(sta[0])
{
if(a[maxn[sta[0]-1]]<=a[maxn[sta[0]]])maxn[sta[0]-1]=maxn[sta[0]];
ans=max(ans,maxn[sta[0]]-sta[sta[0]]+1);
maxn[sta[0]--]=0;
}
printf("%d",ans);
return 0;
}
rp++