题目描述
历史学考后,$MYC$和$ztr$对答案,发现选择题他们没有一道选的是一样的。最后他们都考了个$C$。现在问题来了,假设他们五五开,分数恰好一样(问答题分数也恰好一样,只考虑选择题)。已知考题是$N$道选择题(第$i$题分数为$M(i)$)。问$ztr$和$MYC$做对的题的并有多少种可能?众所周知,历史学考选择题有$25$题,但是$MYC$为了给你降低难度,$n$不超过$20$。
一句话题意:有多少个非空子集,能划分成和相等的两份。
原题见:$USACO 2012 OPEN GOLD subsets$
输入格式
第一行:整数$N$
第$2..1+N$行:第$i+1$行是$M(i)$
输出格式
一个整数表示答案
样例
样例输入:
4
1
2
3
4
样例输出:
3
数据范围与提示
样例解释:
有三个合法的集合:${1,2,3}$,它可以被分割成${1,2}$和${3}$,集合${1,3,4}$,它可以被分割为${1,3}$和${4}$;集合${1,2,3,4}$可以被分割成子集${1,4}$和${2,3}$。
数据范围:
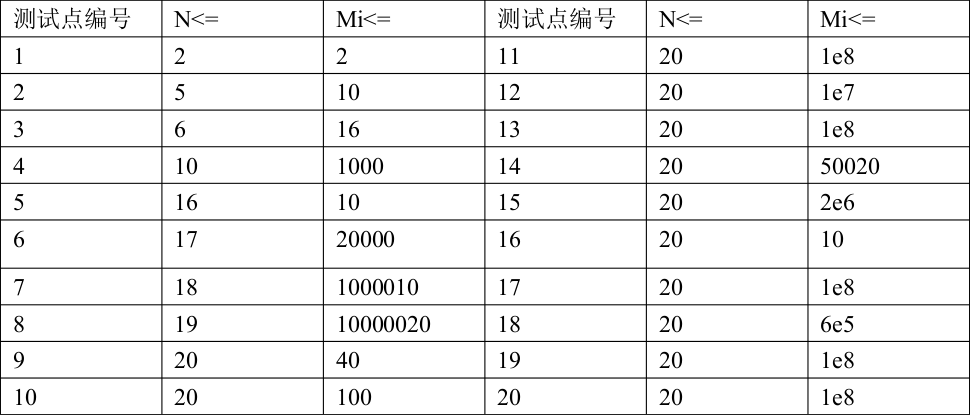
不要问我为什么数据范围这么奇怪。。。因为要给大家送分。。。
题解
又被题意坑死……
先来解释一下题意,题目是要统计所有子集中可以被等分的集合(如果有多种方案,不能重复统计)。
$Theta(n^3)$暴力应该都会打(分为不选,给一个人,给另一个人)。
但是这样显然过不去,考虑$meet in the middle$,先枚举左边$3^{frac{N}{2}}$,再枚举右边$3^{frac{N}{2}}$即可。
时间复杂度:$Theta(6^{frac{N}{2}})$。、
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
const int mod=30000019;
struct rec{int nxt,to,now,val;}e[59050];
int head[300000019],cnt;
int N;
int a[21];
bool vis[1100][1100],v[21];
int ans;
void insert(int now,int val)
{
int key=(val%mod+mod)%mod;
for(int i=head[key];i;i=e[i].nxt)
if(e[i].now==now&&e[i].val==val)return;
e[++cnt].nxt=head[key];
e[cnt].now=now;
e[cnt].val=val;
head[key]=cnt;
}
int ask(int now,int val)
{
int key=(val%mod+mod)%mod,res=0;
for(int i=head[key];i;i=e[i].nxt)
if(e[i].val==val&&!vis[e[i].now][now])
{
vis[e[i].now][now]=1;
res++;
}
return res;
}
void dfs1(int x,int w)
{
if(x>N/2)
{
int now=0;
for(int i=1;i<=N/2;i++)now=now<<1|v[i];
insert(now,w);
return;
}
v[x]=0;dfs1(x+1,w);
v[x]=1;dfs1(x+1,w+a[x]);
v[x]=1;dfs1(x+1,w-a[x]);
}
void dfs2(int x,int w)
{
if(x>N)
{
int now=0;
for(int i=N/2+1;i<=N;i++)now=now<<1|v[i];
ans+=ask(now,w);
return;
}
v[x]=0;dfs2(x+1,w);
v[x]=1;dfs2(x+1,w+a[x]);
v[x]=1;dfs2(x+1,w-a[x]);
}
int main()
{
scanf("%d",&N);
for(int i=1;i<=N;i++)scanf("%d",&a[i]);
dfs1(1,0);
dfs2(N/2+1,0);
printf("%d",ans-1);
return 0;
}
rp++