题目描述
科学家在“无限神机”($Infinity Machine$)找到一个奇怪的机制,这个机制有$N$个元件,有$M$条电线连接这些元件,所有元件都是连通的。两个元件之间可能有多条电线连接。
科学家对这些元件可以任意地设置为“高电压”和“低电压”两种模式,如果一条电线的一端为高电压,另一端为低电压,这条电线就会产生电流。
为了安全的研究“无限神机”,科学家需要找到一条电线,将它的两端设为相同的电压,并且除选择的这条电线外,其它所有电线都有电流(否则就没有研究的价值了)。
有多少条电线满足这样的条件?
输入格式
输入的第一行包含两个正整数$n,m$,表示元件数和电线数。
接下来$m$行,每行两个整数$u,v$,表示元件$u$和元件$v$有一条电线连接
输出格式
输出一个整数,表示有多少条电线满足条件
样例
样例输入1:
4 5
1 2
1 3
1 4
2 4
3 4
样例输出1:
1
样例输入2:
4 4
1 2
2 3
3 2
4 3
样例输出2:
2
数据范围与提示
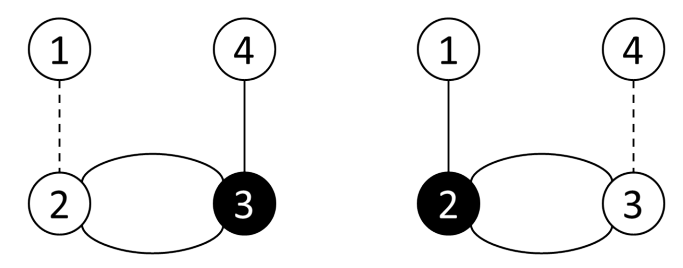
样例$1$解释:
如图,只有电线$(1,4)$满足

样例$2$解释:
电线$(1,2)$和$(3,4)$满足要求
数据范围:
对于$10/%$的数据,满足$nleqslant 1,000,mleqslant 2,000$
对于另外$10/%$的数据,满足$m=n$
对于另外$35/%$的数据,满足$mleqslant n+100$
对于$100/%$的数据,满足$2leqslant nleqslant 100,000,1leqslant mleqslant 200,000$
题解
再一次被语文打倒(可能是我语文太菜了叭~)……
先来解释一下题意,在样例$2$中$2$和$3$之间的边之所以不能设成相同的电压,是因为之后剩下那条边两端的电压就相同了,也就没有电流了。
为方便,不妨将一条电线两端电压设成相同成为“删”掉这条边。
话个图我们便会发现,偶环中的都不能删,如下图中无论删掉哪条边,对面的边两端电压都会相同。
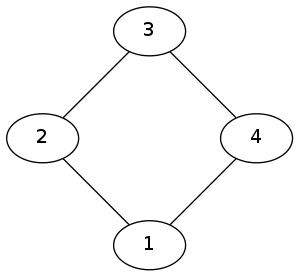
但是,不在偶环里的就一定能删吗?
看下面这一张图$downarrow$
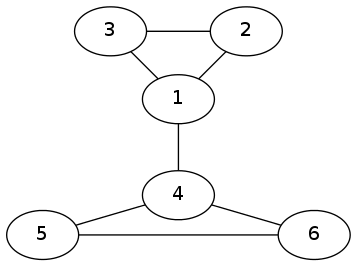
可以发现,$(2,3)$和$(5,6)$互相牵制,都不能删。
于是我们还可以推得,一条边必须能被所有奇环包含并且不被任何偶环包含才能被删。
那么怎么求呢?
其实如果我说利用树上差分思想就不那么难了,先建一棵$DFS$树,剩下的边全部为反祖边,判断环是奇是偶然后分别用两个数组记录即可(设这条边从$u$到$v$,$v$是祖先,在$u$处$--$并在$v$处$++$即可)。
注意数据并没有保证联通!!!
时间复杂度:$Theta(n+m)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to;bool dead;}e[400002];
int head[100001],cnt=1;
int n,m;
int odd[100001],eve[100001],cut[400002],depth[100001],in[100001];
bool vis[100001];
int ans;
void add(int x,int y)
{
e[++cnt].nxt=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void dfs(int x)
{
vis[x]=1;
for(int i=head[x];i;i=e[i].nxt)
{
if(cut[i])continue;
cut[i]=cut[i^1]=1;
if(vis[e[i].to])
{
if((depth[x]-depth[e[i].to])&1){eve[e[i].to]--;eve[x]++;}
else{odd[e[i].to]--;odd[x]++;odd[0]++;}
}
else
{
depth[e[i].to]=depth[x]+1;
in[e[i].to]=i;
dfs(e[i].to);
}
}
}
void dfs(int x,int f)
{
for(int i=head[x];i;i=e[i].nxt)
if(in[e[i].to]==i)
{
dfs(e[i].to,x);
odd[x]+=odd[e[i].to];
eve[x]+=eve[e[i].to];
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
for(int i=1;i<=n;i++)if(!vis[i])dfs(i);
if(odd[0]==1)ans=1;
for(int i=1;i<=n;i++)if(!in[i])dfs(i,0);
for(int i=1;i<=n;i++)
if(in[i]&&odd[i]==odd[0]&&!eve[i])ans++;
printf("%d",ans);
return 0;
}
rp++