1.线性可分
对于一个数据集:
如果存在一个超平面X能够将D中的正负样本精确地划分到S的两侧,超平面如下:

那么数据集D就是线性可分的,否则,不可分。
w称为法向量,决定了超平面的方向;b为位移量,决定了超平面与原点的距离。
样本空间中的任意点x到超平面X的距离(不太熟悉的可以复习高数中空间几何那一章的内容)可以写为:
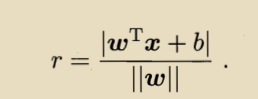
使得下面两式成立的训练样本称为支持向量:

两个异类支持向量(一个等于+1,一个等于-1)到超平面的距离之和为:
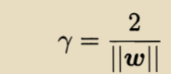
它称之为“间隔”
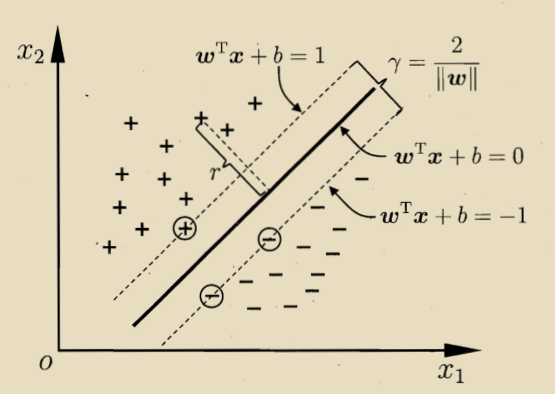
想找到最大间隔的划分超平面,就是使最大:

等价于:
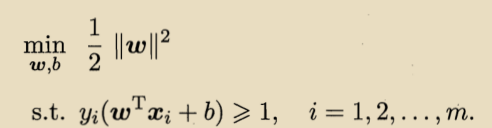
这就是支持向量机的基本模型。
对偶问题:
上式的拉格朗日函数可写为:

其中,
对参数w和b求导可得:
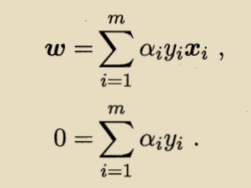
将上式带入到拉格朗日函数中,消去w和b,得到对偶表达式:
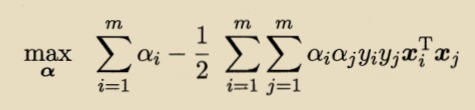
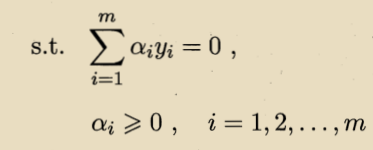
采用SMO算法完成对偶问题的求解:
原始论文地址:http://www-ai.cs.uni-dortmund.de/LEHRE/SEMINARE/SS09/AKTARBEITENDESDM/FOLIEN/Joerg_Nitschke_Sequential_minimal_optimization.pdf
核函数:
对于非线性可分的训练样本通过核函数将原始空间映射到更高维的特征空间来使得样本线性可分。
令表示x映射后的特征向量,那么新的模型可以表示为:
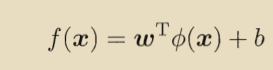
可以得出:
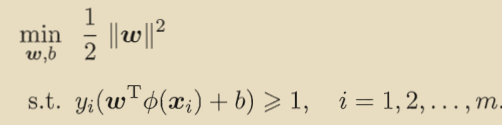
对偶问题表示为:
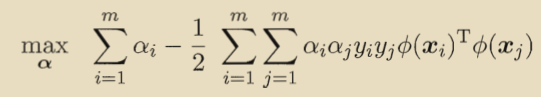
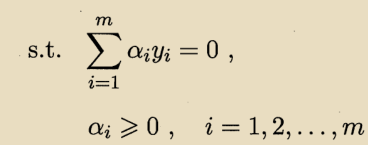
这里涉及到,这是样本
和
映射到高维特征空间后的內积,我们不直接计算
,设计一个函数:
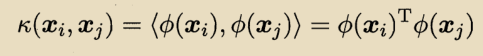
重写为:
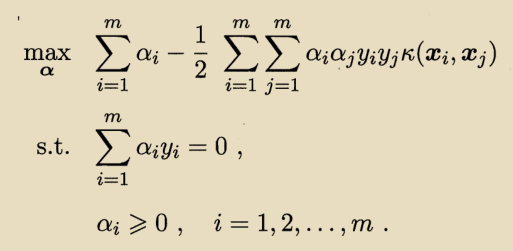
求解出,即可求出模型:
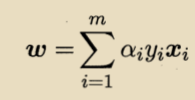
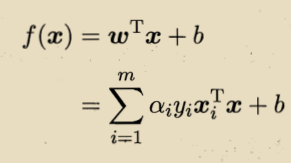

我会在优化理论里面更仔细地分析核函数。
软间隔和正则化:
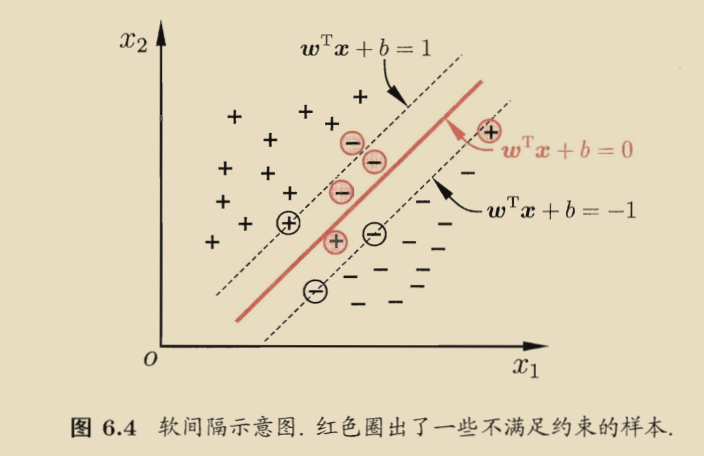
软间隔允许某些样本不满足约束,优化目标可以改写为:

是非凸、非连续的函数,采用其他函数来代替
,称为surrogate loss。通常surrogate loss是凸的连续函数且是
的上界。下面有三种常用的代理损失函数:
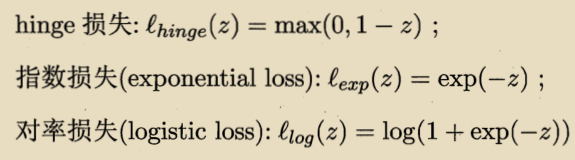
若采用hinge损失:
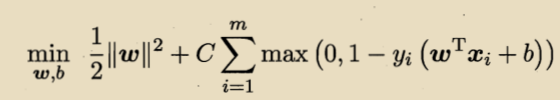
引入松弛变量:
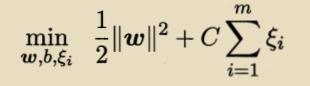

得到拉格朗日函数:
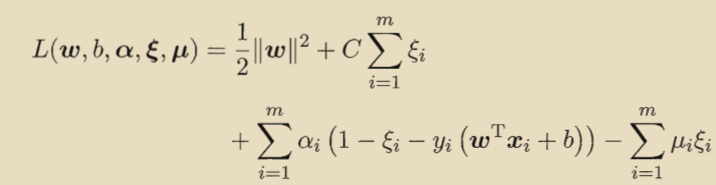
其中是拉格朗日乘子。

对偶问题:
