代码中的变量定义皆是同前面笔记相同
1.PyTorch的nn模块
神经网络的结构与原理相信大家已经非常熟悉,这里不再赘述。
PyTorch有一个专门用于神经网络的完整子模块:torch.nn。该子模块包含创建各种神经网络体系结构所需的构建块。这些构建块在PyTorch术语中称为module(模块),在其他框架中称为layer(层)。
PyTorch模块都是从基类nn.Module继承而来的Python类。模块可以具有一个或多个参数(Parameter)实例作为属性,这些参数就是在训练过程中需要优化的张量(在笔记1的线性模型中即w和b)。模块还可以具有一个或多个子模块(nn.Module的子类)属性,并且也可以追踪其参数。
可以找到一个名为nn.Linear的nn.Module子类,它对其输入进行仿射变换(通过参数属性weight和bias);它就相当于之前在笔记1中的温度计实验中实现的方法。现在,从上次中断的地方开始,将之前的代码转换为使用nn的形式。
import torch.nn as nn
linear_model = nn.Linear(1, 1) # 参数: input size, output size, bias(默认True)
linear_model(t_un_val) # t_un_val为切分出的验证集,并经过了normalization
nn.Linear的构造函数接受三个参数:输入特征的数量,输出特征的数量以及线性模型是否包含偏差(此处默认为True)。例如,如果在输入中同时使用了温度和气压,则在其中输入具有两个特征输入和而输出只有一个特征。
PyTorch的nn.Module及其子类被设计为可以同时处理多个样本。为了容纳多个样本,模型希望输入的第0维为这个批次中的样本数目。 因此,假设你需要对10个样本运行nn.Linear,则可以创建大小为 B x Nin 的输入张量,其中 B 是批次的大小,而 Nin 是输入特征的数量,然后在模型中同时运行:
x = torch.ones(10, 1)
linear_model(x)
下图显示了批处理图像数据的类似的情况。输入尺寸为 BxCxHxW,其中批处理大小(batch size)B为3(狗、鸟和汽车的图像),每张图像通道数C为3(红色,绿色和蓝色),高度 H 和宽度 W 的像素数未指定。
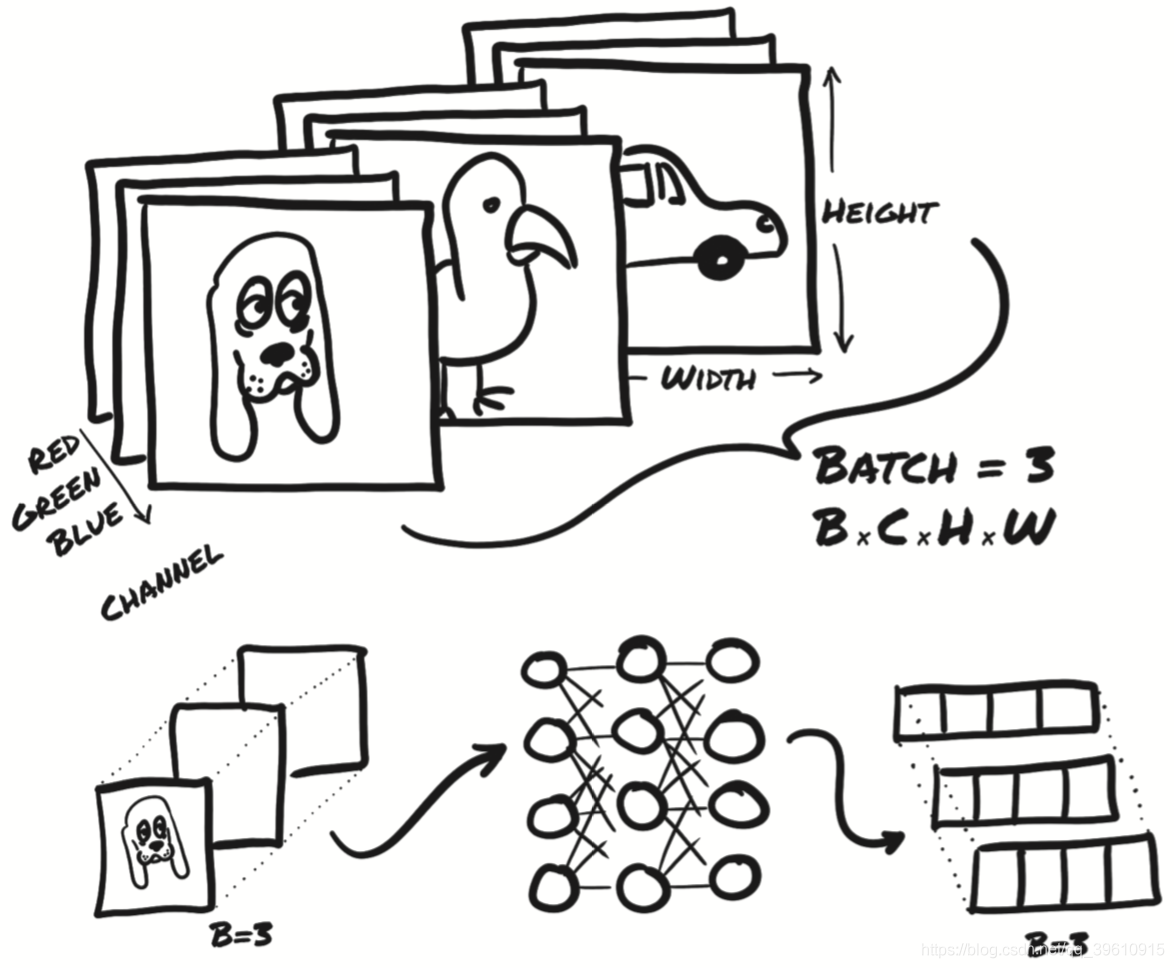
输出是大小为 B x Nout 的张量,其中 Nout 是输出特征的数量——在此例中为四个。
进行此批处理的原因是多方面的。一个主要动机是以使我们充分利用执行计算的计算资源。GPU是高度并行化的,因此在小型模型上的单个输入将使大多数计算单元处于空闲状态。通过提供成批的输入,可以将计算分散到其他闲置的计算单元上,这意味着成批的结果就像单个结果一样能够很快地返回。另一个好处是,某些高级模型将使用整个批次的统计信息,而当批次大小较大时那些统计数据将变得更准确。
回到之前的线性模型,需要将尺寸为 B 的输入reshape为 B x Nin,其中Nin为1。
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1) # 增加一维
t_u = torch.tensor(t_u).unsqueeze(1) #
将之前的手工模型替换为nn.Linear(1,1),然后将线性模型参数传递给优化器:
linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(
linear_model.parameters(), # 获取任何nn.Module或其子模块的参数列表
lr=1e-2)
我们为优化器提供了一个require_grad = True张量列表。所有参数都是用这种方式定义的,因为它们需要通过梯度下降进行优化。调用raining_loss.backward()时,grad将累积在图的叶节点上,这些节点正是传递给优化器的参数。
调用optimizer.step()时,优化器将循环访问每个参数,并按与存储在其grad属性中的值成比例的量对其进行更改。
现在你不再明确地将params传递给model,因为model本身在内部保存有Parameters。
下面来看看修改后的完整代码:
import torch
import torch.optim as optim
import torch.nn as nn
def training_loop(n_epochs, optimizer, model, loss_fn,
t_u_train, t_u_val, t_c_train, t_c_val):
for epoch in range(1, n_epochs+1):
t_p_train = model(t_u_train)
loss_train = loss_fn(t_p_train, t_c_train)
t_p_val = model(t_u_val)
loss_val = loss_fn(t_p_val, t_c_val)
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print('Epoch %d, Training loss %.4f, Validation loss %.4f' % (
epoch, float(loss_train), float(loss_val)))
if __name__ == "__main__":
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0] #实际结果(摄氏度)
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4] #温度计读取的数值
t_c = torch.tensor(t_c).unsqueeze(1) # 将数据增加一维
t_u = torch.tensor(t_u).unsqueeze(1)
# 划分训练集与测试集
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples) #切出20%为测试集
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]
val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]
t_un_train = 0.1 * train_t_u
t_un_val = 0.1 * val_t_u
# 模型
linear_model = nn.Linear(1, 1)# 参数:input size, output size, bias(默认True)
# 优化器
optimizer = optim.SGD(
linear_model.parameters(),
lr = 1e-2)
# 训练循环
training_loop(
n_epochs = 3000,
optimizer = optimizer,
model = linear_model,
loss_fn = nn.MSELoss(), # 不再使用自己定义的loss函数
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = train_t_c,
t_c_val = val_t_c)
还差最后一个步骤:用神经网络代替线性模型作为近似函数。
nn提供了一种通过nn.Sequential容器串联模块的简单方法:
seq_model = nn.Sequential(
nn.Linear(1, 13),
nn.Tanh(),
nn.Linear(13, 1))
该模型将1个输入特征散开为13个隐藏特征,然后将通过tanh激活函数,最后将得到的13个数字线性组合为1个输出特征。
有关nn.Modules参数的一些注意事项:当你检查由几个子模块组成的模型的参数时,可以方便地通过其名称识别参数。这个方法叫做named_parameters:
for name, param in seq_model.named_parameters():
print(name, param.shape)
输出:
0.weight torch.Size([13, 1])
0.bias torch.Size([13])
2.weight torch.Size([1, 13])
2.bias torch.Size([1])
这些都是优化器所需的参数张量。同样,在调用model.backward()之后,所有参数都将被计算其grad,然后优化器会在调用optimizer.step()期间更新参数的值,这与之前的线性模型没有太大不同。毕竟这两个模型都是可微分的模型,可以通过梯度下降进行训练。
实际上,Sequential中每个模块的名称都是该模块在参数中出现的顺序。有趣的是,Sequential还可以接受OrderedDict作为参数,这样就可以给Sequential的每个模块命名:
from collections import OrderedDict
seq_model = nn.Sequential(OrderedDict([
('hidden_linear', nn.Linear(1, 8)),
('hidden_activation'), nn.Tanh(),
('output_linear', nn.Linear(8, 1))
]))
for name, param in seq_model.named_parameters():
print(name, param.shape)
输出:
hidden_linear.weight torch.Size([8, 1])
hidden_linear.bias torch.Size([8])
output_linear.weight torch.Size([1, 8])
output_linear.bias torch.Size([1])
你还可以通过访问子模块来访问特定的参数,就像它们是属性一样:
seq_model.output_linear.bias
输出:
Parameter containing:
tensor([-0.1786], requires_grad=True)
该代码对于检查参数或其梯度(例如在训练期间监视梯度)很有用。
最后画出输入数据(圆形),期望输出(叉号)和显示样本之间行为的连续曲线
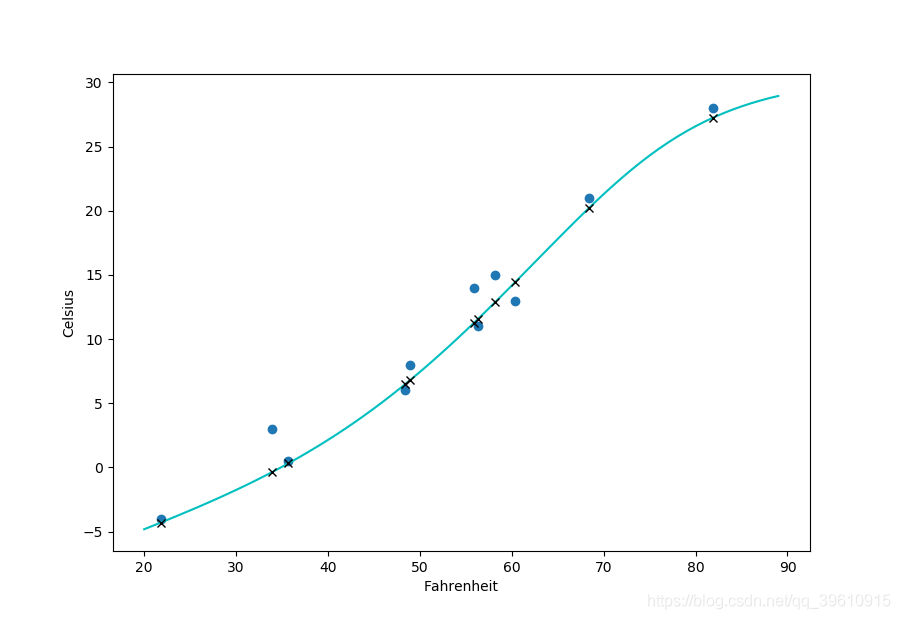
完整代码如下:
import torch
import torch.optim as optim
import torch.nn as nn
from collections import OrderedDict
from matplotlib import pyplot as plt
def training_loop(n_epochs, optimizer, model, loss_fn,
t_u_train, t_u_val, t_c_train, t_c_val):
for epoch in range(1, n_epochs+1):
t_p_train = model(t_u_train)
loss_train = loss_fn(t_p_train, t_c_train)
t_p_val = model(t_u_val)
loss_val = loss_fn(t_p_val, t_c_val)
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print('Epoch %d, Training loss %.4f, Validation loss %.4f' % (
epoch, float(loss_train), float(loss_val)))
if __name__ == "__main__":
# 实际结果(摄氏度)
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
# 温度计读取的数值(单位未知)
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1) # 将数据增加一维
t_u = torch.tensor(t_u).unsqueeze(1)
# 划分训练集与测试集
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]
val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]
t_un_train = 0.1 * train_t_u
t_un_val = 0.1 * val_t_u
seq_model = nn.Sequential(OrderedDict([
('hidden_linear', nn.Linear(1, 8)),
('hidden_activation', nn.Tanh()),
('output_linear', nn.Linear(8, 1))
]))
optimizer = optim.SGD(
seq_model.parameters(),
lr = 1e-3)
training_loop(
n_epochs = 5000,
optimizer = optimizer,
model = seq_model,
loss_fn = nn.MSELoss(), # 不再使用自己定义的loss
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = train_t_c,
t_c_val = val_t_c)
print('output', seq_model(t_un_val))
print('answer', val_t_c)
# 打印出隐藏层线性部分的权重的梯度
print('hidder', seq_model.hidden_linear.weight.grad)
# 绘图
t_range = torch.arange(20., 90.).unsqueeze(1)
fig = plt.figure(dpi = 100)
plt.xlabel("Fahrenheit")
plt.ylabel("Celsius")
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.plot(t_range.numpy(), seq_model(0.1 * t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(), seq_model(0.1 * t_u).detach().numpy(), 'kx')
plt.show()
2.nn的子类
对于更大,更复杂的项目,你需要将nn.Sequential放在一边,转而使用可以带来更大灵活性的东西:将nn.Module子类化。
要实现nn.Module的子类,至少需要定义一个forward()函数,该函数将接收模型输入并返回输出。如果你使用的是torch中的操作,那么autograd会自动处理反向传递。
在第一节中,我们已经使用了nn.Sequential来实现一个神经网络,并且用有序字典而不是列表作为输入为每一层添加标签以作改进。
进一步,可以自己定义nn.Module的子类来完全控制输入数据的处理方式。
import torch
import torch.optim as optim
import torch.nn as nn
from collections import OrderedDict
from matplotlib import pyplot as plt
class SubclassModel(nn.Module):
def __init__(self):
# super()用于调用父类的方法,可用来解决多重继承问题。
super().__init__()
self.hidden_linear = nn.Linear(1, 13)
self.output_linear = nn.Linear(13, 1)
# 需要定义一个forward()函数,该函数将接收模型输入并返回输出
def forward(self, input):
hidden_t = self.hidden_linear(input)
activated_t = torch.tanh(hidden_t) # nn.Tanh对应的函数
output_t = self.output_linear(activated_t)
return output_t
def training_loop(n_epochs, optimizer, model, loss_fn,
t_u_train, t_u_val, t_c_train, t_c_val):
for epoch in range(1, n_epochs+1):
t_p_train = model(t_u_train)
loss_train = loss_fn(t_p_train, t_c_train)
t_p_val = model(t_u_val)
loss_val = loss_fn(t_p_val, t_c_val)
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print('Epoch %d, Training loss %.4f, Validation loss %.4f' % (
epoch, float(loss_train), float(loss_val)))
if __name__ == "__main__":
# 实际结果(摄氏度)
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
# 温度计读取的数值(单位未知)
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1) # 将数据增加一维
t_u = torch.tensor(t_u).unsqueeze(1)
# 划分训练集与测试集
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]
val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]
t_un_train = 0.1 * train_t_u
t_un_val = 0.1 * val_t_u
subclass_model = SubclassModel()
optimizer = optim.SGD(
subclass_model.parameters(),
lr = 1e-3)
training_loop(
n_epochs = 5000,
optimizer = optimizer,
model = subclass_model,
loss_fn = nn.MSELoss(), # 不再使用自己定义的loss
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = train_t_c,
t_c_val = val_t_c)