Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
Note: Do not modify the linked list.
题目含义:判断列表是否有环路,如果有,返回环路的开始节点
思路:定义slow和fast两个指针,fast每次走两步,slow每次走一步,如果fast.next或者fast.next.next为null,链路一定没有环路,否则一定出现了环路。
从第一次相遇以后,slow继续往前走,fast该从头部开始每次一步走,再次相遇时候一定是环路的起点,证明如下:
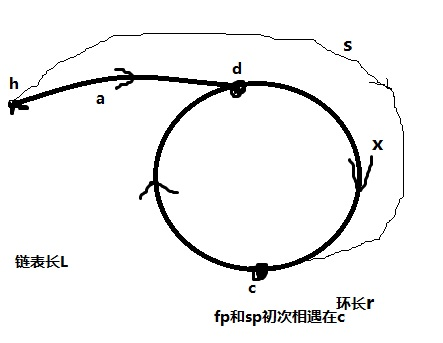
2s = s + nr =>
又因为hd距离为a,dc距离为x,hc距离为s,所以可以得出:
a + x = s (2)
结合(1)和(2)可以得出:
a + x = nr -> a + x = (n-1)r + r -> a + x = (n-1)r + r
-> a = (n-1)r + (r-x)
即此时h到d的距离a等于c到d的距离(r-x)。所以当fp和sp初次相遇在c点的时候,令fp从c点出发,sp指向链表头h,两个同时以步数为1同时出发,则再次相遇的时候即为环的入口节点d。
1 public boolean hasCycle(ListNode head) {
2 if (head == null) return false;
3 ListNode walker = head;
4 ListNode runner = head;
5 while (runner.next !=null && runner.next.next != null)
6 {
7 walker = walker.next;
8 runner = runner.next.next;
9 if (walker == runner) return true;
10 }
11 return false;
12 }
考察点2:返回环路的起点位置
1 public ListNode detectCycle(ListNode head) { 2 ListNode walker = head; 3 ListNode runner = head; 4 while (runner!=null && runner.next!=null ) 5 { 6 walker = walker.next; 7 runner = runner.next.next; 8 if (walker == runner) 9 { 10 while (head!=walker) 11 { 12 head = head.next; 13 walker=walker.next; 14 } 15 return walker; 16 } 17 } 18 return null; 19 }
检查数组是否有环路的方法 287. Find the Duplicate Number
考察点3:判断两个列表是否相交,并且返回第一个相交节点
160. Intersection of Two Linked Lists
考察点4:找出环路中的节点数(环的长度)
思路1:记录下相遇节点存入临时变量tempPtr,然后让slow(或者fast,都一样)继续向前走slow = slow -> next;一直到slow == tempPtr; 此时经过的步数就是环上节点的个数;
1 public int find_cycleLength(ListNode head) { 2 // 方法一: 3 ListNode walker = head; 4 ListNode runner = head; 5 while (runner != null && runner.next != null) { 6 walker = walker.next; 7 runner = runner.next.next; 8 if (walker == runner) { 9 while (head != walker) { 10 head = head.next; 11 walker = walker.next; 12 } 13 walker = walker.next;//walker位环路的开始节点,walker先往前走一步 14 int round = 1; 15 while (walker != head) { 16 walker = walker.next; 17 round++; 18 } 19 return round; 20 } 21 } 22 return 0; 23 }
思路2: 从相遇点开始slow和fast继续按照原来的方式向前走slow = slow -> next; fast = fast -> next -> next;直到二者再次项目,此时经过的步数就是环上节点的个数 。
对于第二种思路,我们可以这样想,结合上面的分析,fast和slow没一次操作都会使得两者之间的距离较少1。我们可以把两者相遇的时候看做两者之间的距离正好是整个环的长度r。因此,当再次相遇的时候所经过的步数正好是环上节点的数目。
1 public int find_cycleLength(ListNode head) { 2 ListNode walker = head; 3 ListNode runner = head; 4 int round=0; 5 while (runner != null && runner.next != null) { 6 walker = walker.next; 7 runner = runner.next.next; 8 if (walker == runner) { 9 walker = walker.next; 10 runner = runner.next.next; 11 round = 1;//walker和runner按照原来的节奏继续走了一轮 12 while (runner != null && runner.next != null) { 13 walker = walker.next; 14 runner = runner.next.next; 15 round++;//walker和runner按照原来的节奏继续走 16 } 17 return round; 18 } 19 } 20 return 0; 21 }
考察点5:如果存在环,求出整个链表的长度:
思路:链表长度L = 起点到入口点的距离 + 环的长度r;
1 public int find_ListLength(ListNode head) { 2 ListNode walker = head; 3 ListNode runner = head; 4 int preLength = 0; 5 int cycleLength = 0; 6 while (runner != null && runner.next != null) { 7 walker = walker.next; 8 runner = runner.next.next; 9 preLength++; 10 if (walker == runner) { 11 while (head != walker) { 12 head = head.next; 13 walker = walker.next; 14 } 15 walker = walker.next;//walker位环路的开始节点,walker先往前走一步 16 cycleLength = 1; 17 while (walker != head) { 18 walker = walker.next; 19 cycleLength++; 20 } 21 break; 22 } 23 } 24 return preLength + cycleLength; 25 }
考察点6:求出环上距离任意一个节点最远的点(对面节点)
思路:
如下图所示,点1和4、点2和5、点3和6分别互为”对面节点“ ,也就是换上最远的点,我们的要求是怎么求出换上任意一个点的最远点。
对于换上任意的一个点ptr0, 我们要找到它的”对面点“,可以这样思考:同样使用上面的快慢指针的方法,让slow和fast都指向ptr0,每一步都执行与上面相同的操作(slow每次跳一步,fast每次跳两步),
当fast = ptr0或者fast = prt0->next的时候slow所指向的节点就是ptr0的”对面节点“。
为什么是这样呢?我们可以这样分析:
如上图,我们想像一下,把环从ptro处展开,展开后可以是无限长的(如上在6后重复前面的内容)如上图。
现在问题就简单了,由于slow移动的距离永远是fast的一般,因此当fast遍历玩整个环长度r个节点的时候slow正好遍历了r/2个节点,
也就是说,此时正好指向距离ptr0最远的点。
思考点7:接触链表中的环
思路:先要找到环路的首节点,然后找到环路的尾节点,然后为节点的next=null

