Long long ago, there is a famous farmer named John. He owns a big farm and many cows. There are two kinds of cows on his farm, one is Friesian, and another one is Ayrshire. Each cow has its own territory. In detail, the territory of Friesian is a circle, and of Ayrshire is a triangle. It is obvious that each cow doesn't want their territory violated by others, so the territories won't intersect.
Since the winter is falling, FJ has to build a fence to protect all his cows from hungry wolves, making the territory of cows in the fence. Due to the financial crisis, FJ is currently lack of money, he wants the total length of the fence minimized. So he comes to you, the greatest programmer ever for help. Please note that the part of fence don't have to be a straight line, it can be a curve if necessary.
Input
The input contains several test cases, terminated by EOF. The number of test cases does not exceed 20.
Each test case begins with two integers N and M(0 ≤ N, M ≤ 50, N + M > 0)which denotes the number of the Friesian and Ayrshire respectively. Then follows N + M lines, each line representing the territory of the cow. Each of the first N lines contains three integers X i, Y i, R i(1 ≤ R i ≤ 500),denotes the coordinates of the circle's centre and radius. Then each of the remaining M lines contains six integers X1 i, Y1 i, X2 i, Y2 i, X3 i, Y3 i, denotes the coordinates of the triangle vertices. The absolute value of the coordinates won't exceed 10000.
Output
For each test case, print a single line containing the minimal fence length. Your output should have an absolute error of at most 1e-3.
Sample Input
1 1
4 4 1
0 0 0 2 2 0
Sample Output
15.66692
Hint
Please see the sample picture for more details, the fence is highlighted with red.
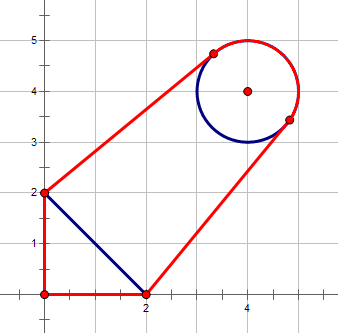
发现类似凸包,但是圆没法解决,做法是把圆拆开来就好了,拆成一千个点,然后套模板,求周长的话,可以直接求没两点距离,想要精确度高一点,可以在圆的点做个标记,是哪个圆,半径是多少,然后求的时候如果是同一个圆就算弧长
直接求距离的
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include <iomanip>
#include<cmath>
#include<float.h>
#include<string.h>
#include<algorithm>
#define sf scanf
#define pf printf
#define mm(x,b) memset((x),(b),sizeof(x))
#include<vector>
#include<queue>
#include<stack>
#include<map>
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=a;i>=n;i--)
typedef long long ll;
typedef long double ld;
typedef double db;
const ll mod=1e9+100;
const db e=exp(1);
const db eps=1e-8;
using namespace std;
const double pi=acos(-1.0);
const int INF=0xfffffff;
struct Point
{
double x,y;
}p[150+50*2000],s[150+50*2000];
int top;
double direction(Point p1,Point p2,Point p3) {
double ans=(p3.x-p1.x)*(p2.y-p1.y)-(p2.x-p1.x)*(p3.y-p1.y);
return ans; }//点2和3,按哪个和点一的角度更小排,相同的话按哪个更近排
double dis(Point p1,Point p2) { return sqrt((p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y)); }
bool cmp(Point p1,Point p2)//极角排序
{
double temp=direction(p[0],p1,p2);
if(fabs(temp)<eps) temp=0;
if(temp<0)return true ;
if(temp==0&&dis(p[0],p1)<dis(p[0],p2))return true;
return false;
}
void Graham(int n)
{
int pos;
double minx,miny;
minx=miny=INF;
for(int i=0;i<n;i++)//找最下面的基点
if(p[i].y<miny||(p[i].y==miny&&p[i].x<minx))
{
minx=p[i].x;
miny=p[i].y;
pos=i;
}
swap(p[0],p[pos]);
sort(p+1,p+n,cmp);
p[n]=p[0];
//sort(p+2,p+n,cmp1);
s[0]=p[0];s[1]=p[1];s[2]=p[2];
top=2;
for(int i=3;i<=n;i++)
{
while(direction(s[top-1],s[top],p[i])>=0&&top>=2)
top--;
s[++top]=p[i] ;
}
}
int main()
{
int n,m;
while(~sf("%d%d",&m,&n))
{
double x,y,r;
int ans=0;
while(m--)
{
sf("%lf%lf%lf",&x,&y,&r);
rep(i,0,2000)
{
p[ans].x=x+r*cos(2.0*pi*i/2000);
p[ans++].y=y+r*sin(2.0*pi*i/2000);
}
}
while(n--)
{
sf("%lf%lf%lf%lf%lf%lf",&p[ans].x,&p[ans].y,&p[ans+1].x,&p[ans+1].y,&p[ans+2].x,&p[ans+2].y);
ans+=3;
}
Graham(ans);
double sum=0;
s[top]=s[0];
rep(i,0,top)
{
sum+=dis(s[i],s[i+1]);
}
pf("%.5lf
",sum);
}
return 0;
}
求弧长的
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include <iomanip>
#include<cmath>
#include<float.h>
#include<string.h>
#include<algorithm>
#define sf scanf
#define pf printf
#define mm(x,b) memset((x),(b),sizeof(x))
#include<vector>
#include<queue>
#include<stack>
#include<map>
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=a;i>=n;i--)
typedef long long ll;
typedef long double ld;
typedef double db;
const ll mod=1e9+100;
const db e=exp(1);
const db eps=1e-8;
using namespace std;
const double pi=acos(-1.0);
const int INF=0xfffffff;
struct Point
{
double x,y,id,r;
}p[150+50*1002],s[150+50*1002];
int top;
double direction(Point p1,Point p2,Point p3) { double ans=(p3.x-p1.x)*(p2.y-p1.y)-(p2.x-p1.x)*(p3.y-p1.y);return ans; }//点2和3,按哪个和点一的角度更小排,相同的话按哪个更近排
double dis(Point p1,Point p2) { return sqrt((p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y)); }
bool cmp(Point p1,Point p2)//极角排序
{
double temp=direction(p[0],p1,p2);
if(fabs(temp)<eps) temp=0;
if(temp<0)return true ;
if(temp==0&&dis(p[0],p1)<dis(p[0],p2))return true;
return false;
}
void Graham(int n)
{
int pos;
double minx,miny;
minx=miny=INF;
for(int i=0;i<n;i++)//找最下面的基点
if(p[i].y<miny||(p[i].y==miny&&p[i].x<minx))
{
minx=p[i].x;
miny=p[i].y;
pos=i;
}
swap(p[0],p[pos]);
sort(p+1,p+n,cmp);
p[n]=p[0];
s[0]=p[0];s[1]=p[1];s[2]=p[2];
top=2;
for(int i=3;i<=n;i++)
{
while(direction(s[top-1],s[top],p[i])>=0&&top>=2)
top--;
s[++top]=p[i] ;
}
}
int main()
{
int n,m;
while(~sf("%d%d",&m,&n))
{
double x,y,r;
int ans=0;
int ID=1;
while(m--)
{
sf("%lf%lf%lf",&x,&y,&r);
rep(i,0,1000)
{
p[ans].id=ID;
p[ans].r=r;
p[ans].x=x+r*cos(2.0*pi*i/1000);
p[ans++].y=y+r*sin(2.0*pi*i/1000);
}
ID++;
}
while(n--)
{
sf("%lf%lf%lf%lf%lf%lf",&p[ans].x,&p[ans].y,&p[ans+1].x,&p[ans+1].y,&p[ans+2].x,&p[ans+2].y);
p[ans].id=0;
p[ans+1].id=0;
p[ans+2].id=0;
ans+=3;
}
Graham(ans);
double sum=0;
rep(i,0,top)
if(s[i].id>0&&(s[i].id==s[(i+1)%top].id))
sum+=1.0*s[i].r*2*pi/1000.0;
else
sum+=dis(s[i],s[(i+1)%top]);
pf("%.5lf
",sum);
}
return 0;
}