题目
Description
传说中的暗之连锁被人们称为 Dark。 Dark 是人类内心的黑暗的产物,古今中外的勇者们都试图打倒它。经过研究,你发现 Dark 呈现无向图的结构,图中有 N 个节点和两类边,一类边被称为主要边,而另一类被称为附加边。 Dark 有 N – 1条主要边,并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。另外,Dark 还有 M 条附加边。你的任务是把 Dark 斩为不连通的两部分。一开始 Dark的附加边都处于无敌状态,你只能选择一条主要边切断。一旦你切断了一条主要边,Dark 就会进入防御模式,主要边会变为无敌的而附加边可以被切断。但是你的能力只能再切断 Dark 的一条附加边。现在你想要知道,一共有多少种方案可以击败 Dark。注意,就算你第一步切断主要边之后就已经把 Dark 斩为两截,你也需要切断一条附加边才算击败了 Dark
Input
第一行包含两个整数 N 和 M。
之后 N – 1 行,每行包括两个整数 A 和 B,表示 A 和 B 之间有一条主要边。
之后 M 行以同样的格式给出附加边。
N≤100 000,M≤200 000。数据保证答案不超过 2^31 – 1
Output
输出一个整数表示答案
Sample Input
4 1
1 2
2 3
1 4
3 4
Sample Output
3
思路:
这是一道树上差分
锯题可知,首先将主要边构成一棵树,如果再将附加边(x,y)加入则会构成一个环,所以不能这样;
如果第一次选择切断主要边,那么第二步就要切断附加边;
所以,我们可以将附加边(x,y)两点的路径覆盖主要边的次数统计出来;
1。如果,主要边被覆盖了零次,那么说明,任何一条附加边与这条边切断都可以分成两部分;
2。如果,主要边被覆盖了一次,那么说明,只有一条附加边与这条边切断都可以分成两部分;
3。如果,主要边被覆盖了两次,那么说明,这条边切断后不能分成两部分;
具体如图:
(黑色代表主要边,红色代表附加边)
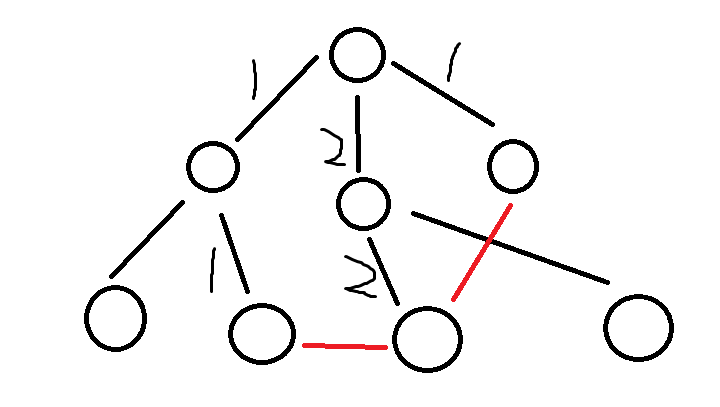
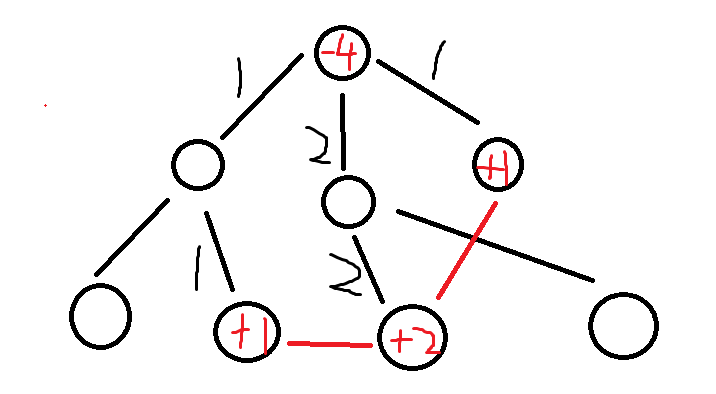
然后,我们可以求出,两个附件边的点,的最近公共祖先;
将最近公共祖先点上的权值减2,将两个点的权值加1;如图二所示;
为什么是这样加减呢;
我们知道 一个数组 x-y的权值加 d,就相当于 它的差分数组的 a[x]+d , a[y+1]-d (不知道的,自己上网搜)
那么,这是每一次覆盖次数加一,然后每个点都和公共祖先有一条边,所以最近公共祖先点上的权值减2,将两个点的权值加1;
树上差分还是有点区别的,这样理解就好了;
然后定义f[x],代表以x为根节点,的所有子节点,包括自己的权值和;
那么f[x]就表示,x与它父节点之间的边的覆盖次数;
最后,如果f[x]==0,ans+=m(m代表附加边的数量)
如果f[x]==1,,ans++
要注意的是,f[x] 如果x是1(根节点),答案ans不需要改变
代码
#include<bits/stdc++.h> using namespace std; typedef long long ll; inline ll read() { ll a=0,f=1; char c=getchar(); while (c<'0'||c>'9') {if (c=='-') f=-1; c=getchar();} while (c>='0'&&c<='9') {a=a*10+c-'0'; c=getchar();} return a*f; } ll n,m,ans; ll head[500001],f[500001]; ll dep[500001],dp[500001][21]; struct sbbbbbb { ll to,stb; }a[500001]; ll s=0; inline void insert(ll x,ll y) { s++; a[s].to=y; a[s].stb=head[x]; head[x]=s; } inline void dfs(ll x,ll fa) { dep[x]=dep[fa]+1; for(ll i=head[x];i;i=a[i].stb) { ll xx=a[i].to; if(xx==fa) continue; dp[xx][0]=x; dfs(xx,x); } } inline ll lca(ll x,ll y) { if(dep[x]<dep[y]) swap(x,y); for(ll i=20;i>=0;i--) if(dep[dp[x][i]]>=dep[y]) x=dp[x][i]; if(x==y) return x; for(ll i=20;i>=0;i--) if(dp[x][i]!=dp[y][i]) x=dp[x][i],y=dp[y][i]; return dp[x][0]; } inline void findout(ll x,ll fa) { for(ll i=head[x];i;i=a[i].stb) { ll xx=a[i].to; if(xx==fa) continue; findout(xx,x); f[x]+=f[xx]; } if(x!=1) { if(f[x]==0)//如果f[x]==0,ans+=m ...思路中讲得很清楚了 ans+=m; if(f[x]==1)//如果f[x]==1,ans++ ...思路中讲得很清楚了 ans++; } } int main() { n=read();m=read(); for(ll i=1;i<=n-1;i++) { ll x=read(),y=read(); insert(x,y); insert(y,x);//将主要边,构成一棵树 } dfs(1,0); for(ll j=1;j<=20;j++) for(ll i=1;i<=n;i++) dp[i][j]=dp[dp[i][j-1]][j-1];//求lca的操作 for(ll i=1;i<=m;i++) { ll x=read(),y=read(); ll sum=lca(x,y); f[sum]-=2; f[x]++;f[y]++;//差分统计...思路中讲得很清楚了 } findout(1,0); printf("%lld",ans); }