二叉苹果树的题面(多叉情况）

题目

Description

有一棵苹果树，如果树枝有分叉，一定是分2叉（就是说没有只有1个儿子的结点）。
这棵树共有N个结点（叶子点或者树枝分叉点），编号为1-N，树根编号一定是1。
    我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有4个树枝
的树：
    2    5
    ＼  ／
       3       4
       ＼  ／
         1

 

现在这颗树枝条太多了，需要剪枝。但是一些树枝上长有苹果。

给定需要保留的树枝数量，求出最多能留住多少苹果。注意树根不能剪没了哟。

Input

第1行2个数，N和Q(1<=Q<=N，I<N<=IOO)。
N表示树的结点数，Q表示要保留的树枝数量。
接下来N-I行描述树枝的信息。 每行3个整数，前两个是它连接的结点的编号。第3个数是这根树枝上苹果的数量。 每根树枝上的苹果不超过30000个。

Output

一个数，最多能留住的苹果的数量。

Sample Input

5 2
1 3 1
1 4 10
3 2 20
3 5 20 

Sample Output

21

---

思路：

二叉解析

https://www.cnblogs.com/wzx-RS-STHN/p/13388044.html

多叉解析

原题是二叉的，所以每次只要访问左子节点和右子节点就可以了；

多叉情况，我们就可以访问，一个子节点和除这颗子树的其他部分；

什么意思呢？我们设dp[x][i]表示，以x为根，保留i 条边，最多能留住的苹果；

枚举k 表示子节点xx为根，保留 k 条边，最多能留住的苹果；

那么

dp[x][i]=max(dp[x][i], dp[xx][k]+dp[x][i-k-1]+a[i].v);

dp[x][j-k-1],表示除了xx这个子树，还保留了j-k-1 条边；

为什么要减一呢？因为xx与x 之间也有条边相连；

+a[i].v 表示加上xx与x 之间这条边上的苹果;

如图：

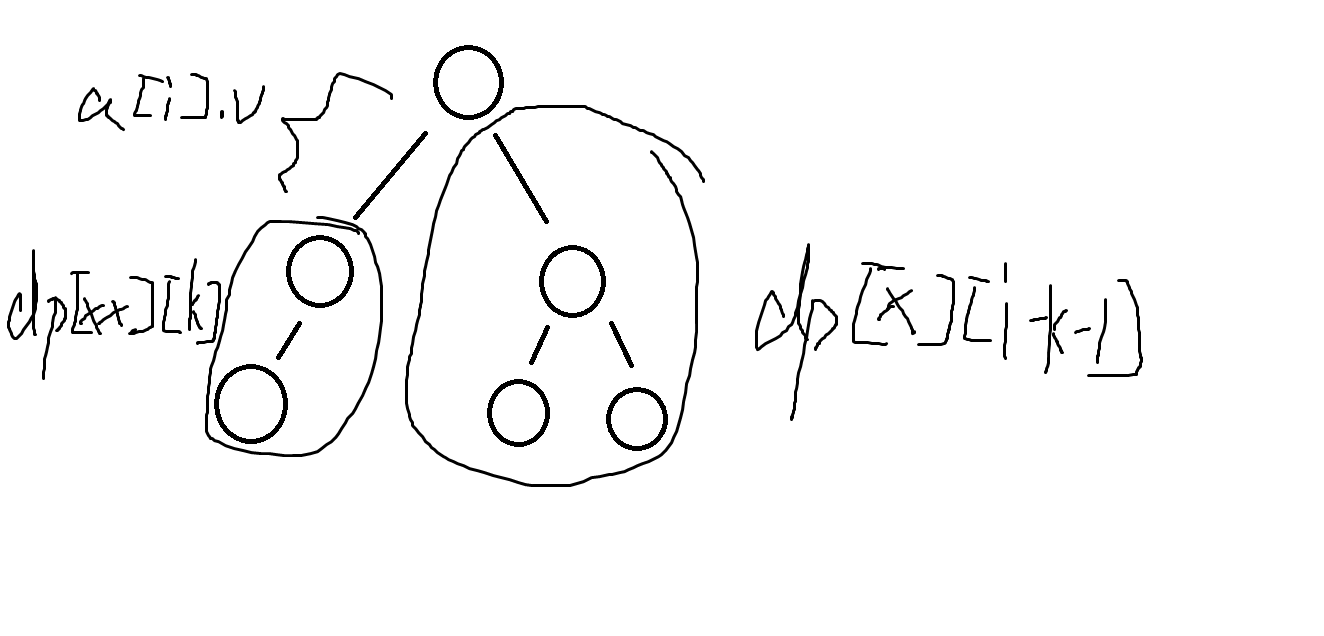
所以，讲得够清楚了吧，还展现了我的高超画艺

代码：

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
inline ll read()
{
    ll a=0,f=1; char c=getchar();
    while (c<'0'||c>'9') {if (c=='-') f=-1; c=getchar();}
    while (c>='0'&&c<='9') {a=a*10+c-'0'; c=getchar();}
    return a*f;
}
ll n,q;
ll head[401],dp[401][410],dep[401];
struct ljj
{
    ll stb,to,v;
}a[601];
ll s=0;
inline void insert(ll x,ll y,ll z)//连边 
{
    s++;
    a[s].stb=head[x];
    a[s].to=y;
    a[s].v=z;
    head[x]=s;
}
inline void dfs(ll x,ll fa)
{
    for(ll i=head[x];i;i=a[i].stb)
    {
        ll xx=a[i].to;
        if(xx==fa)
            continue;
        dfs(xx,x);
        dep[x]+=dep[xx]+1;//dep存的是每个节点下面相连的边数；
        for(ll j=min(q,dep[x]);j>=1;j--)// 减少一点for循环，不加亦可以AC 
                                     //xx 减去的边数不可能多于 xx 下面的所有边 
        for(ll k=0;k<=min(j-1,dep[xx]);k++)//同上，不予解释 
           dp[x][j]=max(dp[x][j],dp[xx][k]+dp[x][j-k-1]+a[i].v);//思路中讲的dp方程 
    }
}
int main()
{
    n=read();q=read();
    for(ll i=1;i<n;i++)
    {
        ll x=read(),y=read(),z=read();
        insert(x,y,z);
        insert(y,x,z);//连边 
    }
    dfs(1,0);
    printf("%lld
",dp[1][q]);
}