https://www.luogu.org/problem/P3435
这题目中文翻译的有毒
首先翻译一下题目:
-
如果存在串 B ( B 可以为空) ,使得 A=PB ,那么称 P 是 A 的前缀。
-
如果 A!= P 并且 P 是 A 的前缀,那么称 P 是 A 的 proper 前缀。
-
如果 Q 是 A 的 proper 前缀,并且 A是 QQ 的前缀,那么称 Q 是 A 的周期。
-
如果 Q 是 A 的所有周期中长度最大的那个,那么称 Q 是 A 的最大周期。特殊的,如果 A 不存在周期,那么 A的最大周期为空串。
-
给出串 S ,求 S 的所有前缀的最大周期长度之和。
抄的题解; -
这是一道让我们深入了解KMP算法精髓的好题。
题目中的“匹配前缀”我们可以这样理解:
在A的前缀中,把这个前缀再叠加一遍后就把A包括进来,如图:
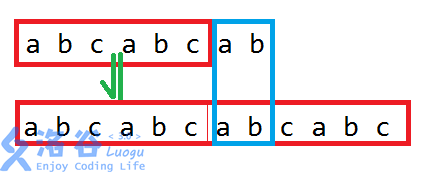
那么,"abcabcab"的最长匹配子串应该是"abcabc",长度为6。
我们设第一个图中字符串为S,第二个字符串为SS,显然有S[6..8]=SS[6..8]=SS[1..2]=S[1..2]。
于是我们得到规律,匹配前缀子串满足KMP算法中“前缀等于后缀”的性质,
我们要使子串最长,那么这个匹配长度应该尽可能小。
但是KMP只能求出每个前缀串的最长匹配长度,如果要求出最短匹配长度,
我们可以一直递推next[i],next[next[i]]...,直到为0.
最后,类似求next时的递推方法,我们可以递推short来提高效率。
答案记得long long,否则只有40分。
code by std:
#include <bits/stdc++.h>
#define MAX (1000000+50)
using namespace std;
int size,nxt[MAX];
char s[MAX];
unsigned long long ans;//记得开long long
int main()
{
ios::sync_with_stdio(0);
cin.tie(0); cin>>size>>(s+1);
for (register int i=2,j=0; i<=size; i++)
{
while (j && s[i]!=s[j+1]) j=nxt[j];
if (s[i]==s[j+1]) j++; nxt[i]=j;
}//KMP求解next数组
for (register int i=2,j=2; i<=size; i++,j=i)
{
while (nxt[j]) j=nxt[j]; //递推求最短匹配长度
if (nxt[i]) nxt[i]=j; //修改next[i]的值
ans+=i-j;//统计答案
}
cout<<ans<<endl;
return 0;
}