排序算法,基本的高级语言都有一些提供。C语言有qsort()函数,C++有sort()函数,java语言有Arrays类(不是Array)。用这些排序时,都可以写自己的排序规则。
Java API对Arrays类的说明是:此类包含用来操作数组(比如排序和搜索)的各种方法。
1.对基本数据类型的数组的排序
说明:(1)Arrays类中的sort()使用的是“经过调优的快速排序法”;
(2)比如int[],double[],char[]等基数据类型的数组,Arrays类之只是提供了默认的升序排列,没有提供相应的降序排列方法。
(3)要对基础类型的数组进行降序排序,需要将这些数组转化为对应的封装类数组,如Integer[],Double[],Character[]等,对这些类数组进行排序。(其实还不如先进行升序排序,自己在转为将序)。
用默认的升序对数组排序
函数原型:static void sort(int[] a) 对指定的 int 型数组按数字升序进行排序。
static void sort(int[] a, int fromIndex, int toIndex) 对指定 int 型数组的指定范围按数字升序进行排序。
源代码解释:
/**
* Sorts the specified array into ascending numerical order.
*
* <p>Implementation note: The sorting algorithm is a Dual-Pivot Quicksort
* by Vladimir Yaroslavskiy, Jon Bentley, and Joshua Bloch. This algorithm
* offers O(n log(n)) performance on many data sets that cause other
* quicksorts to degrade to quadratic performance, and is typically
* faster than traditional (one-pivot) Quicksort implementations.
*
* @param a the array to be sorted
*/
第一部分:
首先介绍排序里面会调用的插入排序,什么时候会调用这段代码,在代码的最后面有解释
下面我来具体讲解这段代码,INSERTION_SORT_THRESHOLD是是否采用插入排序的阈值
代码中设置为47,当小于排序长度小于47时,调用下面这块代码
leftmost是boolean类型,如果是true表示是从第一个位置开始往后排序,如果不是,说明是从中间任意位置开始排序
如果leftmost是true的时候,采用最原始的插入排序方法,
如果是false的时候,采用优化的插入排序方法,pair insertion sort,每次对两个数据进行插入,提高了效率
/**
* Sorts the specified range of the array by Dual-Pivot Quicksort.
*
* @param a the array to be sorted
* @param left the index of the first element, inclusive, to be sorted
* @param right the index of the last element, inclusive, to be sorted
* @param leftmost indicates if this part is the leftmost in the range
*/
private static void sort(int[] a, int left, int right, boolean leftmost) {
int length = right - left + 1;
// Use insertion sort on tiny arrays
if (length < INSERTION_SORT_THRESHOLD) {
if (leftmost) {
/*
* Traditional (without sentinel) insertion sort,
* optimized for server VM, is used in case of
* the leftmost part.
*/
for (int i = left, j = i; i < right; j = ++i) {
int ai = a[i + 1];
while (ai < a[j]) {
a[j + 1] = a[j];
if (j-- == left) {
break;
}
}
a[j + 1] = ai;
}
} else {
/*
* Skip the longest ascending sequence.
*/
do {
if (left >= right) {
return;
}
} while (a[++left] >= a[left - 1]);
/*
* Every element from adjoining part plays the role
* of sentinel, therefore this allows us to avoid the
* left range check on each iteration. Moreover, we use
* the more optimized algorithm, so called pair insertion
* sort, which is faster (in the context of Quicksort)
* than traditional implementation of insertion sort.
* 具体执行过程:上面的do-while循环已经排好的最前面的数据
*(1)将要插入的数据,第一个值赋值a1,第二个值赋值a2,
*(2)然后判断a1与a2的大小,使a1要大于a2
*(3)接下来,首先是插入大的数值a1,将a1与k之前的数字一一比较,直到数值小于a1为止,把a1插入到合适的位置,注意:这里的相隔距离为2
*(4)接下来,插入小的数值a2,将a2与此时k之前的数字一一比较,直到数值小于a2为止,将a2插入到合适的位置,注意:这里的相隔距离为1
*(5)最后把最后一个没有遍历到的数据插入到合适位置
*/
for (int k = left; ++left <= right; k = ++left) {
int a1 = a[k], a2 = a[left];
if (a1 < a2) {
a2 = a1; a1 = a[left];
}
while (a1 < a[--k]) {
a[k + 2] = a[k];
}
a[++k + 1] = a1;
while (a2 < a[--k]) {
a[k + 1] = a[k];
}
a[k + 1] = a2;
}
int last = a[right];
while (last < a[--right]) {
a[right + 1] = a[right];
}
a[right + 1] = last;
}
return;
}
。。。。。。//这里只截取了长度小于INSERTION_SORT_THRESHOLD的时候,大于的时候比较难,没具体分析
/**下面是INSERTION_SORT_THRESHOLD的解释
* If the length of an array to be sorted is less than this
* constant, insertion sort is used in preference to Quicksort.
*/
private static final int INSERTION_SORT_THRESHOLD = 47;
}
第二部分:
当要排队列长度小于QUICKSORT_THRESHOLD并且大于INSERTION_SORT_THRESHOLD时,用双基准快速排序方法,
这部分的代码就是上面。。。。没有显示的部分,具体的原理同双基准快速排序
第三部分:
如果要排序的队列长读大于INSERTION_SORT_THRESHOLD,采用合并排序方法
/**
* If the length of an array to be sorted is less than this
* constant, Quicksort is used in preference to merge sort.
*/
private static final int QUICKSORT_THRESHOLD = 286;
import java.util.Arrays;public class ArraysSort_11 {
public static void main(String args[])
{
int[] a={1,4,-1,5,0};
Arrays.sort(a);
//数组a[]的内容变为{-1,0,1,4,5}
for(int i=0;i<a.length;i++)
System.out.print(a[i]+" ");
}
}
2.对复合数据类型的数据的排序
函数原型: (1)public static<T> void sort(T[] a,Comparator c) 根据指定比较器产生的顺序对指定对象数组进行排序。
(2)public static<T> void sort(T[] a,int fromIndex,int toIndex,Comparator c) 根据指定比较器产生的顺序对指定对象数组的指定范围进行排序。
说明:这个两个排序算法是“经过调优的合并排序”算法。
源码:
其中的两个API
public static <T> void sort(T[] a, Comparator<? super T> c) {
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, c);
else
TimSort.sort(a, c);
}
public static <T> void sort(T[] a, int fromIndex, int toIndex,
Comparator<? super T> c) {
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, fromIndex, toIndex, c);
else
TimSort.sort(a, fromIndex, toIndex, c);
}
核心代码调用的是相同的代码
如果:LegacyMergeSort.userRequested为真时:
执行下面代码:
这里c可以为null,如果为null,则调用默认的比较器进行比较,否则调用用户指定的比较器进行比较。
下面是改进版的合并排序
执行步骤如下:
(1)如果比较的长度小于INSERTIONSORT_THRESHOLD插入排序的阈值,直接调用传统的插入排序进行比较
(2)当大于插入排序的阈值时,采用合并排序算法,这里有个改进的地方,加亮部分,如果已经排好序的,不再进行比较,而是直接复制过去,提高效率
private static void mergeSort(Object[] src,
Object[] dest,
int low, int high, int off,
Comparator c) {
int length = high - low;
// Insertion sort on smallest arrays
if (length < INSERTIONSORT_THRESHOLD) {
for (int i=low; i<high; i++)
for (int j=i; j>low && c.compare(dest[j-1], dest[j])>0; j--)
swap(dest, j, j-1);
return;
}
// Recursively sort halves of dest into src
int destLow = low;
int destHigh = high;
low += off;
high += off;
int mid = (low + high) >>> 1;
mergeSort(dest, src, low, mid, -off, c);
mergeSort(dest, src, mid, high, -off, c);
// If list is already sorted, just copy from src to dest. This is an
// optimization that results in faster sorts for nearly ordered lists.
if (c.compare(src[mid-1], src[mid]) <= 0) {
System.arraycopy(src, low, dest, destLow, length);
return;
}
// Merge sorted halves (now in src) into dest
for(int i = destLow, p = low, q = mid; i < destHigh; i++) {
if (q >= high || p < mid && c.compare(src[p], src[q]) <= 0)
dest[i] = src[p++];
else
dest[i] = src[q++];
}
}
如果LegacyMergeSort.userRequested为假时,
调用TimSort.sort方法,如果c为null,还是调用上面的方法,
否则调用比较器进行比较
代码实例:
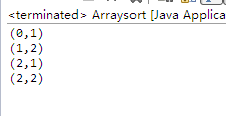
package aa;import java.util.Arrays;import java.util.Comparator;public class Arraysort {
Point[] arr;
Arraysort(){
arr=new Point[4]; //定义对象数组arr,并分配存储的空间
for(int i=0;i<4;i++)
arr[i]=new Point();
}
public static void main(String[] args) {
Arraysort sort=new Arraysort();
sort.arr[0].x=2;sort.arr[0].y=1; //初始化,对象数组中的数据
sort.arr[1].x=2;sort.arr[1].y=2;
sort.arr[2].x=1;sort.arr[2].y=2;
sort.arr[3].x=0;sort.arr[3].y=1;
Arrays.sort(sort.arr, new MyComprator()); //使用指定的排序器,进行排序
for(int i=0;i<4;i++) //输出排序结果
System.out.println("("+sort.arr[i].x+","+sort.arr[i].y+")");
}
}class Point{
int x;
int y;
}//比较器,x坐标从小到大排序;x相同时,按照y从小到大排序class MyComprator implements Comparator {
public int compare(Object arg0, Object arg1) {
Point t1=(Point)arg0;
Point t2=(Point)arg1;
if(t1.x != t2.x)
return t1.x>t2.x? 1:-1;
else
return t1.y>t2.y? 1:-1;
}
}
执行输出: