软件工程第三次作业

目录

• 一、题目要求
• 二、核心代码
• 三、判定/条件覆盖测试程序设计流程图
• 四、测试样例
• 五、单元测试结果

一、题目要求

• 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
  例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
  

二、核心代码

package SumCoding;
import java.util.Scanner;

public class SC {
	
	public static void main(String[] args) {
		Scanner scan=new Scanner(System.in);
        int i,n;
        int[] num=new int[100];
        n=scan.nextInt();        
        for(i=0;i<n;i++)
            num[i]=scan.nextInt();
        int result = sum(num);
        System.out.println("连续子元素的最大和为："+result);
        scan.close();
	}
	
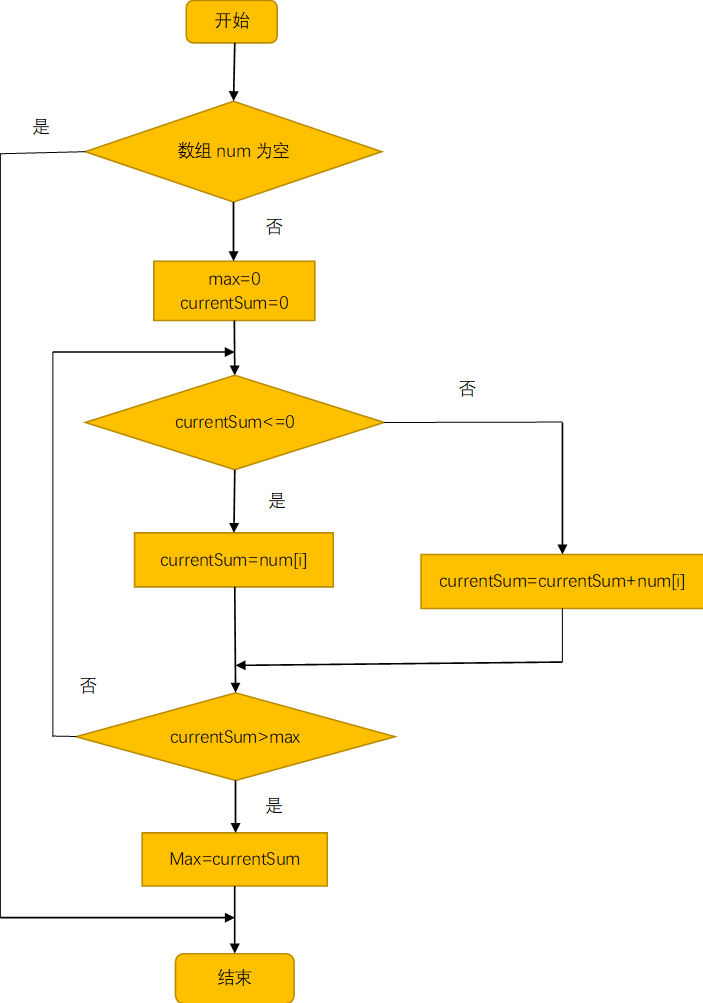
	public static int sum(int[] num) {
        if (num.length==0 || num==null) {
            return 0;
        }
        int currentSum = 0;     
        int max = 0;           
        for (int i = 0; i <num.length; i++) {
            if(currentSum<=0){     
                currentSum = num[i];     
            }else{
                currentSum = currentSum + num[i];   
            }
            if(currentSum>max){         
                max = currentSum;      
            }
        }
        return max;
    } 

}

Github代码链接

三、判定/条件覆盖测试程序设计流程图

四、测试样例

public class SCTest {

	@Test
	public void testSum1() {
		assertEquals(0,new SC().sum(new int [] {}));
	}

	@Test
	public void testSum2() {
		assertEquals(20,new SC().sum(new int[] {-2,11,-4,13,-5,-2} ));
	}
	
	@Test
	public void testSum3(){
		assertEquals(0, new SC().sum(new int[] {-1,-2,-3,-4,-5,-6} ));
	}

}

五、单元测试结果