卷积神经网络CNN

卷积神经网络组成:  INPUT -> CONV -> ReLU -> POOL -> FC

卷积操作:

• 输入大小为：W1 x H1 x D1
• 指定的超参数：filter个数（K），filter大小（F），步长（S），边界填充（P）

输出：

• W2 = (W1 - F + 2P)/S + 1
• H2 = (H1 - F + 2P)/S + 1
• D2 = K

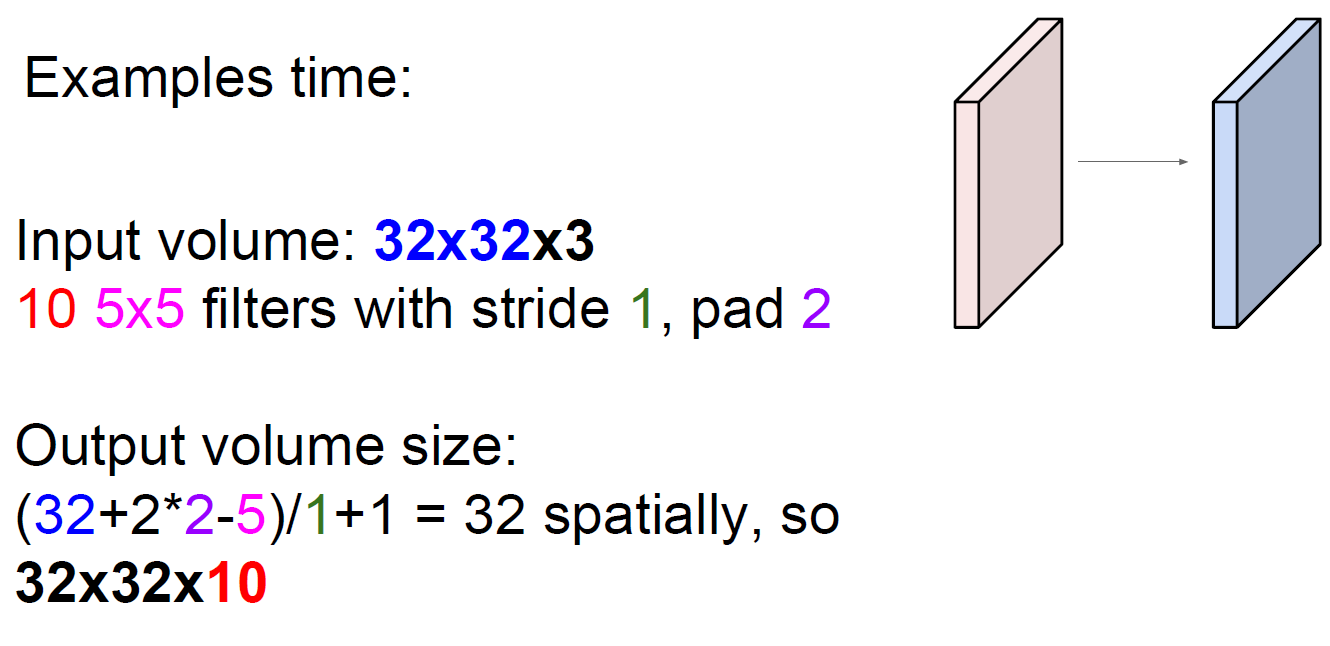
Input: rows * rows *  channels, N filter_rows*filter_rows filters with stride=stride, pade=pad

Output:  output_rows = (rows+2*pad-filter_rows)/stride + 1

MAX POOLING更常用，AVE POOLING用得少了

反向传播：

对于CONV，其每一层正向传播：out = x * w + b，

其中：

• out.size == [depth_out, out_height, out_width)
• w.size == [depth_out, depth_x, filter_height, filter_width]
• x.size == [sample, depth_x, height, width]
• b.size == [depth_out]

则对应的反向传播计算：

dw[k_depth_out, k_depth_x, :, :] =
sum {
x[k_sample, k_depth_x,
 (k_height+stride*k_out_height):(k_height+stride*k_out_height+stride),
 (k_width +stride*k_out_width ):(k_width +stride*k_out_width +stride)]
* dout[k_depth_out, k_out_height, k_out_width] * STEP
}

???   dout = x * dw => dw = dout/x   ???

因为CNN并不是假设dout均匀分配给各个x[k]，而是假设x[k]越大，特征越显著，对应的w[k]贡献就越大，此时修改对应的w[k]，效果也越显著

关于POOL操作

对于均值POOL，反向传播平均分配给前一级网络。

对于MAX POOL，只返回到最大位置

如何巧妙设计网络结构

设：R为filter半径，N为out put depth

用小半径，多层处理，参数个数 = (2*R+1) * N = 2*R*N + N

用一个卷积层，参数个数 = (2*R*N+1)^2 = 4*R^2*N^2 + 4*R*N + 1

明显参数个数， 分多层小filter << 用一个大卷积层

但根据计算，predict的运算量，分多层小filter > 用一个大卷积层

非线性程度，运算量分多层小filter > 用一个大卷积层