原题链接 https://www.luogu.org/problemnew/show/P1440
今天下午本来想刷一道ST表的题温习一下RMQ问题,点开算法标签找到了这个题。
草草看了一下题面,果然是RMQ问题,只不过询问区间的方式不一样了qwq。
自信的我打上了ST表模板,可是只有80分,有两个点MLE了:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m; int a[2000001],f[2000001][20]; int main() { n=read();m=read(); for(int i=1;i<=n;i++) { a[i]=read(); f[i][0]=a[i]; } for(int j=1;(1<<j)<=n;j++) for(int i=1;i+(1<<j)-1<=n;i++) f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]); cout<<0<<endl; if(n==1) return 0; for(int i=2;i<=n;i++) { int l=i-m; int r=i-1; if(l<1) l=1; int len=r-l+1; int t=(int)(double)((double)log(len)/log(2.0)); printf("%d ",min(f[l][t],f[r-(1<<t)+1][t])); } return 0; }
急忙看了一眼n的范围:
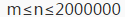
显然f[2000001][20]爆掉了空间!
然后想了好多种方法来节省空间:将数组定义为short类型的,用滚动数组……之类的神奇东西,可是好像还是不大行。
旁边的gh学长瞅了一眼,“这不是单调队列模板题嘛?”他不屑地说。
可是我们还没学单调队列呢,于是gh学长就给我讲起了单调队列qwq。
具体讲的啥早忘辽,只知道这个队列里的元素要么单调递增,要么单调递减。(这不是定义嘛)然后gh学长敲了一下单调队列的代码,没做出来!然后他就找了一篇单调队列的题解让我看(大雾
刚看完一些资料,学得也不是很深,给不懂的同学浅谈一下单调队列吧(说的不对的地方麻烦各位大佬指出,我会及时改正的):
定义:
单调队列,即单调递减或单调递增的队列。
用途——解决“滑动窗口”的问题:
如下图,给出一个长度为n的序列A,求A中所有长度为m的连续子序列的最大值。下图中假设n=7,m=3。
这题只需枚举每个连续子序列,使用单调队列得出最大值即可。
浅谈原理及实现:
对于此题,它要求的是每个滑动窗口的最大值,所以我们要创一个单调递减的单调队列!
1.当单调队列有新元素插入时,我们将队列里所有比该元素小的元素弹出队列(维护递减的性质);
2.然后判断队首是否已经超出滑动窗口的范围,若超出,则将该元素从队首弹出;
3.直接返回队首元素;
单调队列的几个操作:
1.弹出队首元素:q.pop_front();
2.弹出队尾元素:q.pop_back();
3.将元素插到队尾:q.push_back();
4.访问队首元素下标:q.front();
5.访问队尾元素下标:q.back();
6.判断队列是否为空:q.empty();
对于这个题应该就用到这么多了吧。
这个题的滑动窗口是[i-m,i-1],是不包含当前点i的,所以一个很自然的想法就是枚举每个点去维护它的前一个点;
AC代码:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> //提供单调队列的函数库 using namespace std; struct member //定义结构题比较方便 { int id,value; //id是下标,value是权值 }a[2000008]; int read() //快读 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m; deque<member> q; //定义一个结构体类型的单调队列q,还是递增队列,来保证队首元素是最小值 int main() { n=read();m=read(); for(int i=1;i<=n;i++) { a[i].value=read(); a[i].id=i; } cout<<0<<endl; //第一个永远是0 if(n==1) return 0; //n==1直接结束程序 for(int i=2;i<=n;i++) { while(!q.empty()&&q.back().value>=a[i-1].value) q.pop_back(); //从队尾开始找,一直将权值比上一个元素大的全部从队尾弹出,这里维护的是上一个点 q.push_back(a[i-1]);//将上一个元素入队 while(q.front().id<i-m) q.pop_front(); //将不在滑动窗口的范围内的元素全部从队首弹出 printf("%d ",q.front().value); //此时队首元素肯定是符合条件的最小值了,直接用printf输出,cout输出会TLE三个点qwq } return 0; }
当然,我也是一条有想法的咸鱼!!!我也有个不自然的想法,那就是:我们不必让每个点去维护上一个点,让它们管好自己就行了:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> //提供单调队列的函数库 using namespace std; struct member //定义结构题比较方便 { int id,value; //id是下标,value是权值 }a[2000008]; int read() //快读 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m; deque<member> q; //定义一个结构体类型的单调队列q,还是递增队列,来保证队首元素是最小值 int main() { n=read();m=read(); for(int i=1;i<=n;i++) { a[i].value=read(); a[i].id=i; } cout<<0<<endl; //第一个永远是0 if(n==1) return 0; //n==1直接结束程序 q.push_back(a[1]); //手动将第一个元素入队 for(int i=2;i<=n;i++) { while(!q.empty()&&q.back().value>=a[i].value) q.pop_back(); //从队尾开始找,一直将权值比该元素大的全部从队尾弹出,这里维护的是当前点 while(q.front().id<i-m) q.pop_front(); //将不在滑动窗口的范围内的元素全部从队首弹出 printf("%d ",q.front().value); //此时队首元素肯定是符合条件的最小值了,直接用printf输出,cout输出会TLE三个点qwq q.push_back(a[i]);//调换一下入队的顺序,把它调在输出之后就不会造成影响了 } return 0; }
但是我都将a数组的范围改到了3e6还是蜜汁RE,好奇怪哦~

另外再附上单调队列的板子题:P1886 滑动窗口
这里我是用的两个单调队列,一个维护最大值(递减),一个维护最小值(递增),然后就解决问题啦,挺快的:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> //提供单调队列的函数库 using namespace std; struct member //定义结构题比较方便 { int id,value; //id是下标,value是权值 }a[1000008]; int read() //快读 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,m; int maxn[1000001],minn[1000001]; deque<member> q; int main() { n=read();m=read(); for(int i=1;i<=n;i++) { a[i].value=read(); a[i].id=i; } for(int i=1;i<=n;i++) { while(!q.empty()&&q.back().value>=a[i].value) q.pop_back(); q.push_back(a[i]); while(q.front().id<i-m+1) q.pop_front(); if(i>=m) printf("%d ",q.front().value); } cout<<endl; while(!q.empty()) q.pop_back(); for(int i=1;i<=n;i++) { while(!q.empty()&&q.back().value<=a[i].value) q.pop_back(); q.push_back(a[i]); while(q.front().id<i-m+1) q.pop_front(); if(i>=m) printf("%d ",q.front().value); } return 0; }