P1310 表达式的值

原题链接 https://www.luogu.org/problemnew/show/P1310

water_lift 一波讲解，然后我们就会了这个题，然后我们就要写博客啦QwQ~

这是个布尔表达式基计数问题。

这个其实⊕就是“|”或运算，×就是“&”与运算。

我们将这个式子通俗得看成：x&y 和 x|y

我们设x0是使x为0的方案数，x1是使x为1的方案数；y0是使y为0的方案数，y1是使y为1的方案数；

使x&y为1的方案数？为0的方案数？

使x|y为1的方案数？为0的方案数？

不难发现：

使x&y为1，那么x和y都要为1，所以方案数为x1∗y1。

使x&y为0，那么x和y不都为1，所以方案数为x1∗y0+x0∗y1+x0∗y0。

使x|y为1的方案数为x1∗y1+x0∗y1+x1∗y0，为0的方案数为x0∗y0。

然后我们发现给出的式子一个特别烦的东东就是：   有括号

为了去掉括号，我们可以考虑将题目输入的中缀表达式给它换成后缀表达式（后缀表达式的好处就是式子中没有括号！）

肿么换呢？这确实是一个难题，还好我们找到了这样一个方法（由于太蒟还不会证正确性）：

遍历中缀表达式：

1. 遇到数字，直接放入答案序列

2. 遇到左括号，入栈

3. 遇到右括号，把栈顶到上一个左括号的元素依次出栈并放入答案序列
4. 遇到乘号，入栈
5. 遇到加号，从栈顶开始弹出这段连续的乘号，并放入答案序列，最后加号入栈

6. 最后把栈里剩下的元素依次放入答案序列

为什么是正确的呢？贴一下water_lift的模拟过程（想要更丰富的展现？请看water_lift的博客）：

 

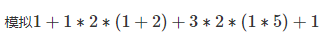
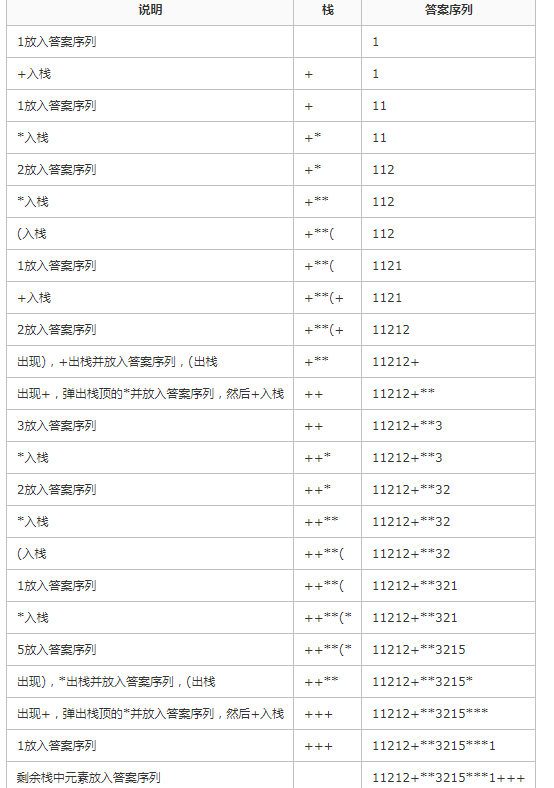
那么有了后缀表达式，这么求值？

这个想必大家都会了，我们用栈就能轻松搞定qwq：

遇到数字入栈，遇到运算符号就取出栈顶的两个元素，将它们进行该运算符的运算后再入栈。

The last question：

题目要求的是使得表达式为0的方案数，那么在哪填数字？

看一下样例： 

 +（*）

很显然就是在这几个标红的位置填数字啦：

_+（_*_）

So，我们可以总结一下在哪里填数字： 式子最前面一定要填个数字（你见哪个式子是符号打头？），然后“+”和“×”后面要填一个数字！

到这里咱们就可以食用代码啦：

#include <bits/stdc++.h>
using namespace std;
stack<char> fh;                                 //中缀表达式转后缀表达式的时候所要用到的存符号的栈 
stack<int> zero;                                //一个存使表达式为0的方案数的栈 
stack<int> one;                                 //一个存使表达式为1的方案数的栈 
string houxu;                                   //转化后的后缀表达式 
char ch[100001];                                //存输入的字符串 
int n,l0,l1,r0,r1;                              
//这里l0就是上文的x0，l1是x1，r0是y0，r1是y1 
const int mod=10007;
int main()
{
    scanf("%d",&n);
    scanf("%s",ch+1);                           //ch+1是让它从下标为1开始读的     
    houxu.push_back('n');                       //后缀表达式的最前头要有个数字，用字符'n'来表示这里应该填数字 
    for(int i=1;i<=n;i++)
    {
        if(ch[i]=='('||ch[i]=='*')              //如果是'('或'*'，正常入符号栈 
        {
            fh.push(ch[i]);
        }
        if(ch[i]=='+')                          //如果是'+'，要把符号栈栈顶的'*' 都放入后缀表达式的后面 
        {
            while(!fh.empty()&&fh.top()=='*')
            {
                houxu.push_back(fh.top());
                fh.pop();
            }
            fh.push(ch[i]);
        }
        if(ch[i]==')')                          //如果是')'，则要把'('和')'之间的符号放入后缀表达式的后面         
        {
            while(fh.top()!='(')
            {
                houxu.push_back(fh.top());
                fh.pop();
            }
            fh.pop();                           //弹出左括号 
        }
        if(ch[i]!='('&&ch[i]!=')') houxu.push_back('n');   //如果不是括号，也就是说如果是'+'或'*'，那么就要在后面填一个数字 
    }
    while(!fh.empty())                          //将符号栈中剩余的符号全部放入后缀表达式  
    {
        houxu.push_back(fh.top());
        fh.pop();
    }
    for(int i=0;i<houxu.size();i++)             //可以看成是后缀表达式求值 
    {
        char c=houxu[i];
        if(c=='n')                              //如果这里该填数字   
        {
            zero.push(1);                       //该数字填0的方案有1种 
            one.push(1);                        //该数字填1的方案有1种 
        }
        else                                    //如果是符号 
        {
            l0=zero.top();zero.pop();           //弹出一个使l为0的方案数 
            l1=one.top();one.pop();             //弹出一个使l为1的方案数 
            r0=zero.top();zero.pop();           //弹出一个使r为0的方案数
            r1=one.top();one.pop();             //弹出一个使r为1的方案数
            if(c=='*')                          //&运算 
            {
                one.push((l1*r1%mod)%mod);      //两个都为1 
                zero.push((l0*r0%mod+l1*r0%mod+l0*r1%mod)%mod);  //不都为1 
            }
            else                                //|运算 
            {
                zero.push((l0*r0%mod)%mod);     //两个都为0 
                one.push((l0*r1%mod+l1*r0%mod+l1*r1%mod)%mod);   //不都为0 
            }
        }
    }
    printf("%d",zero.top()%mod);                //最后剩下的就是使整个表达式为0的方案数 
    return 0;
}