原题链接 https://www.luogu.com.cn/problem/P1244
闲话时刻
CSP-S 考炸了,心情低落,开始水起了橙题 我觉得 dp 这一类的题在 CSP-S 中考的挺常见的(当然还有树论),作为一个 dp 菜鸡准备开始重新学 dp,暂且由这个题来作为新起点吧qwq 。
题目大意
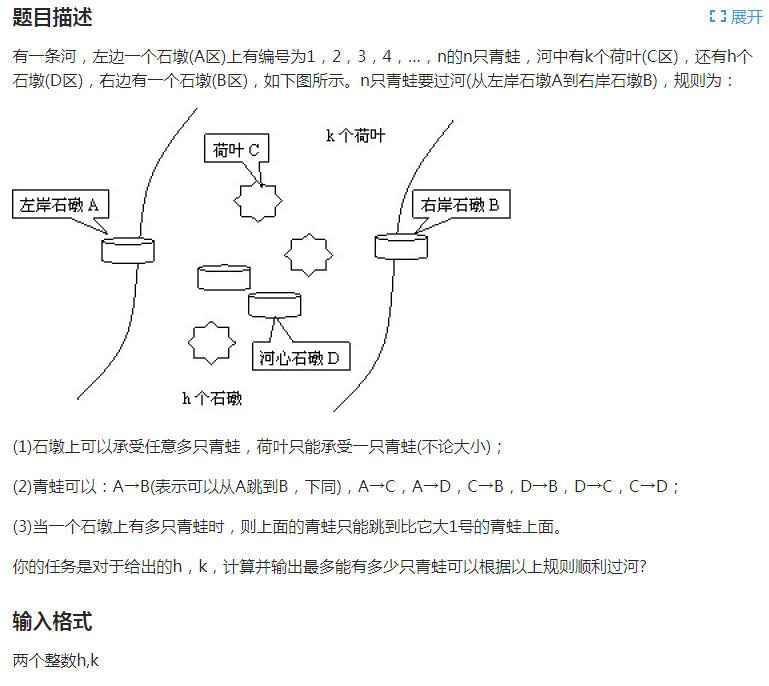
河的两岸各有一只石墩 A , B,河中有 h 个石墩和 k 个荷叶,问最多能有多少只青蛙能够顺利过河,过河规则如下:
1. 每个石墩可以像叠罗汉一样载若干只青蛙,但是每只青蛙只能踩在比它编号大 1 的青蛙的头上;每个荷叶只能载一只青蛙;
2. 只有当一只青蛙的头上没有青蛙时,才能移动这只青蛙;
3. 一开始在石墩 A 上的时候,青蛙们排列符合在石墩上的规则,且都跳到石墩后也要满足该规则;
4. 青蛙可以直接从石墩 A 跳到石墩 B;
5. 只要从石墩 A 跳出去后,就不能再回到石墩 A 了;一旦跳到石墩 B,就不能再跳回去了;
6. 本题的青蛙不会游泳;
题解
这道挺有意思的,同时还颇具思维难度,我们可以从简单到复杂依次去考虑;
我们设一个答案数组:ans [ i ][ j ] 表示 h=i,k=j 时的答案;
① 先看 h=0 的情况:
也就是河中只有荷叶,没有石墩的情况,看一个简单的例子:
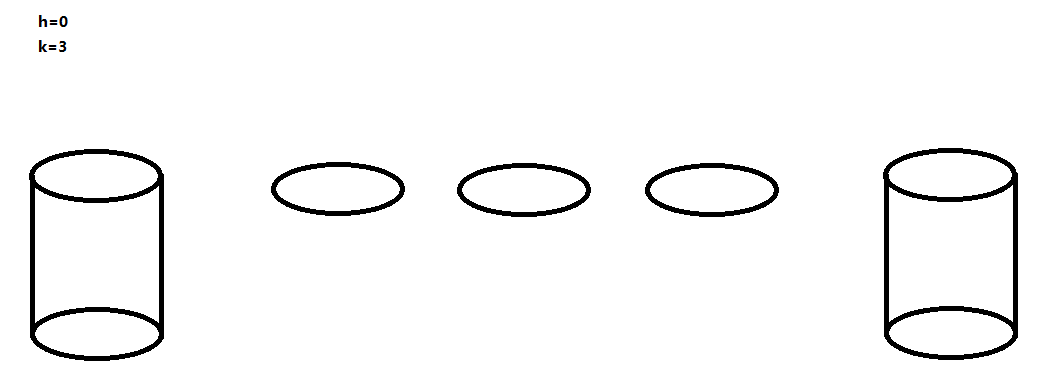
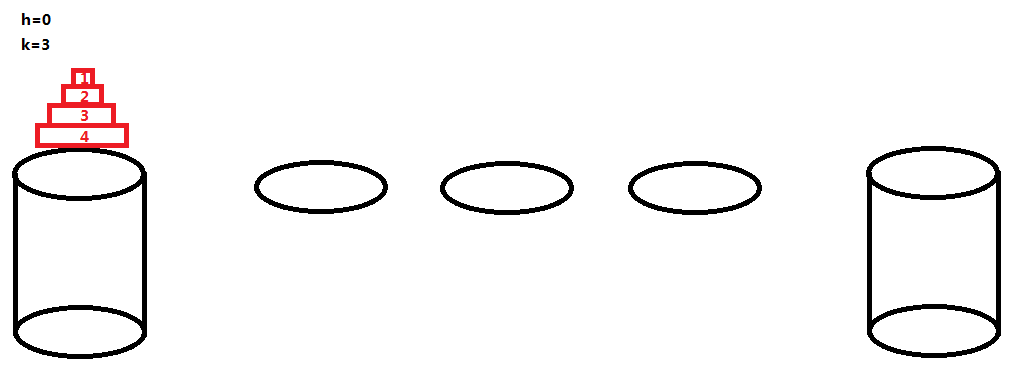
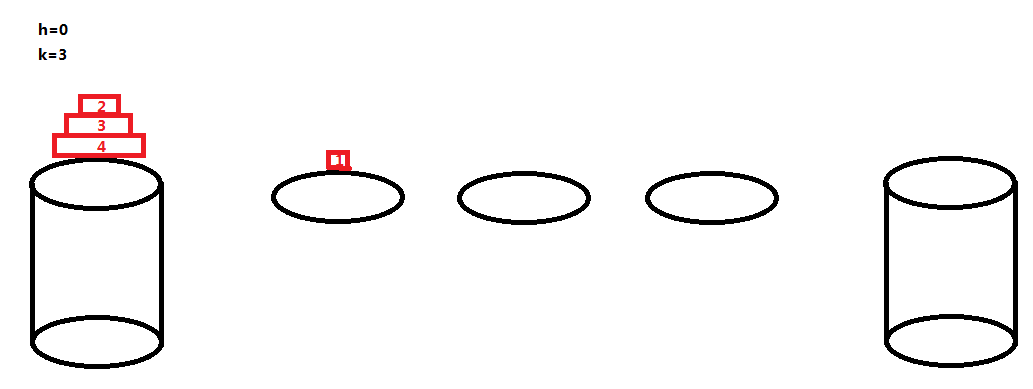
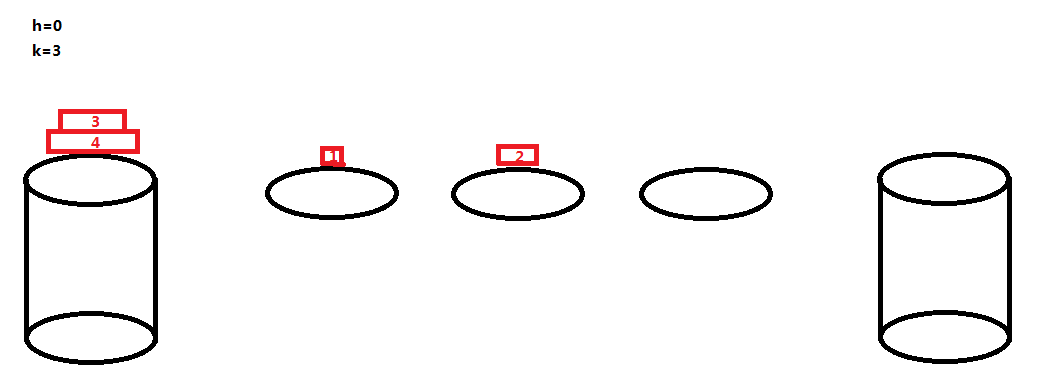
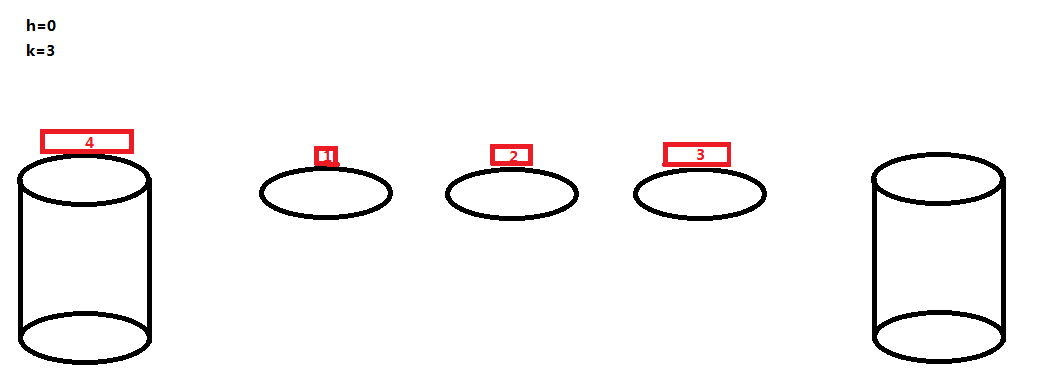
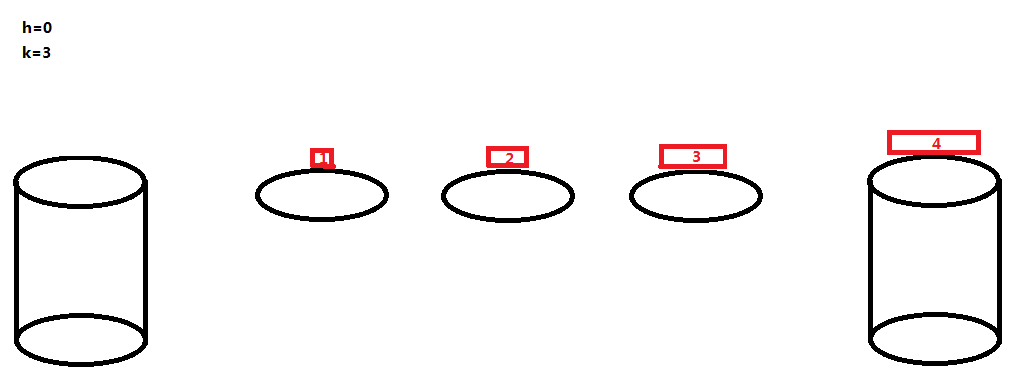

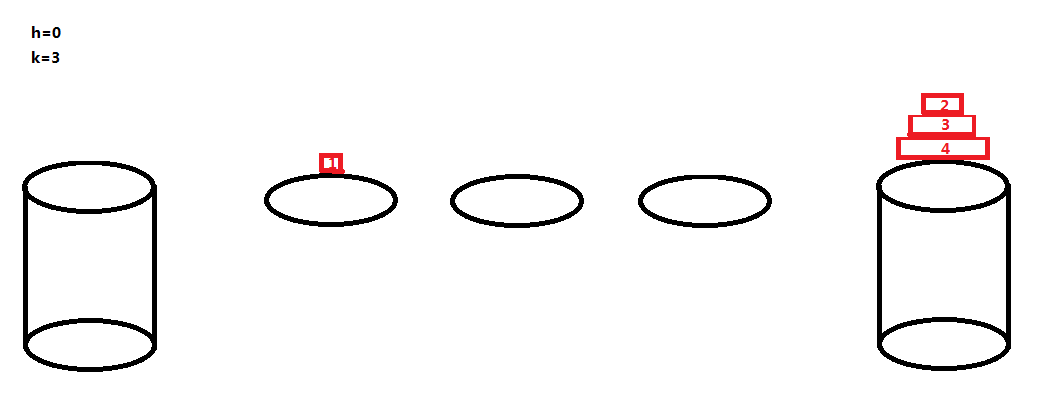
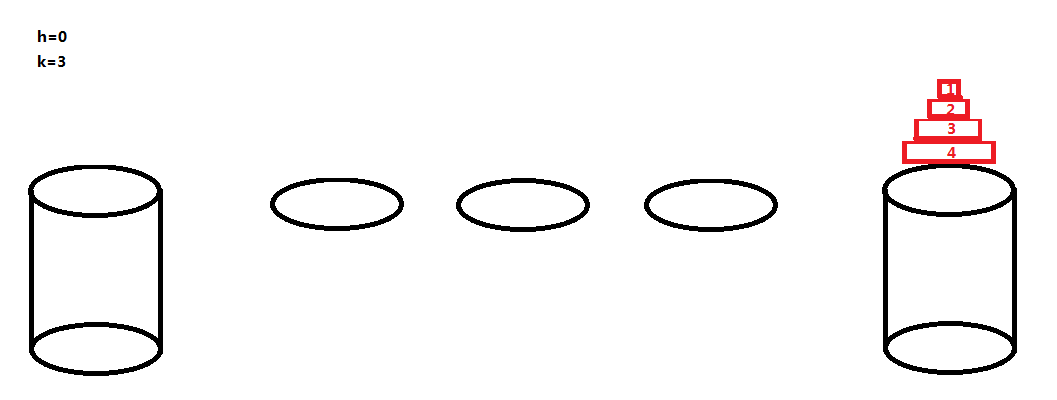
ans [ 0 ][ 3 ] = 4;
我们可以发现:
当 h=0 的时候,每个荷叶可以作为一只青蛙的落脚点,然后一开始的石墩 A 也可以作为一只青蛙的落脚点(且只能是编号最大的那只青蛙的落脚点),这样得话一共能有 k+1 只青蛙顺利过河 。
ans [ 0 ][ k ] = k+1;
② 看 h≠0 的情况:
还是上面的那个例子,只不过河里多了一个石墩,那么怎么办呢?
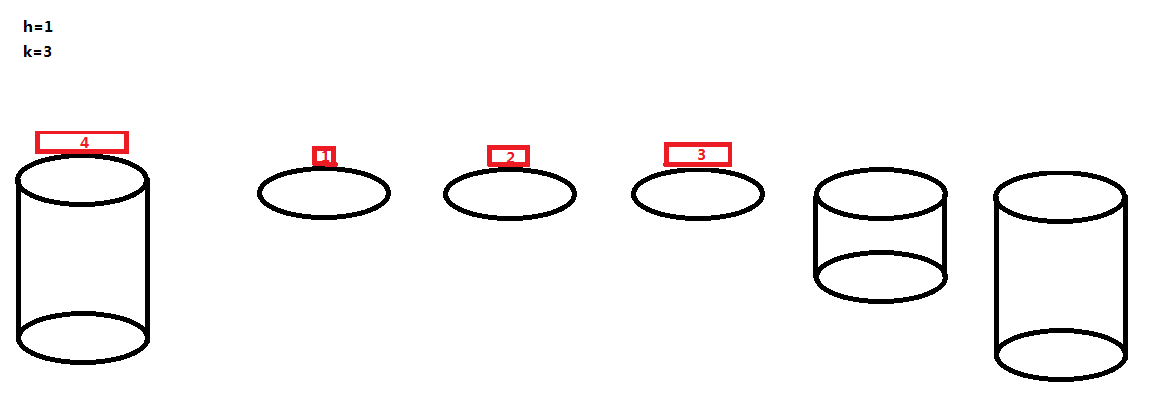
其实,河中的石墩和河岸的石墩 B 都是能够载若干只青蛙的,且它们两个的排列规则是相同的,我们不妨暂且将河中的这一个石墩钦定为石墩 B,然后像刚刚那样的跳法将这四只青蛙都跳到河中石墩来:
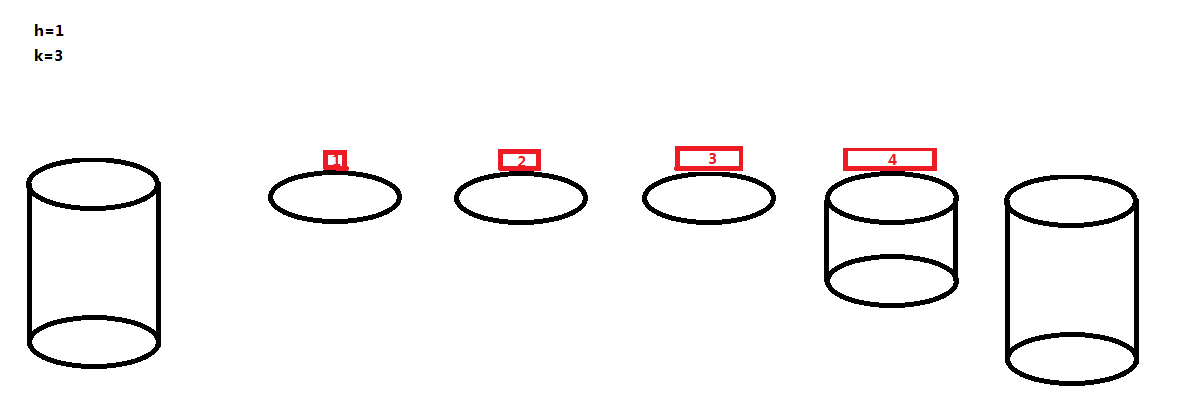
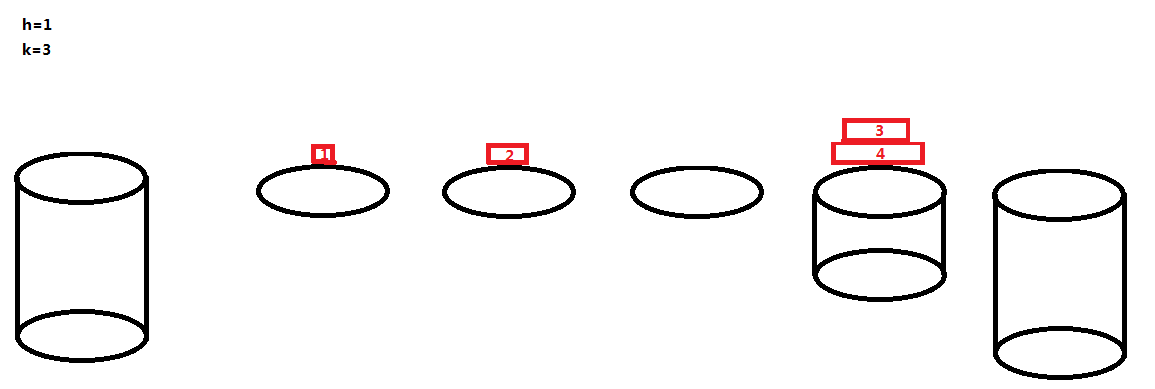
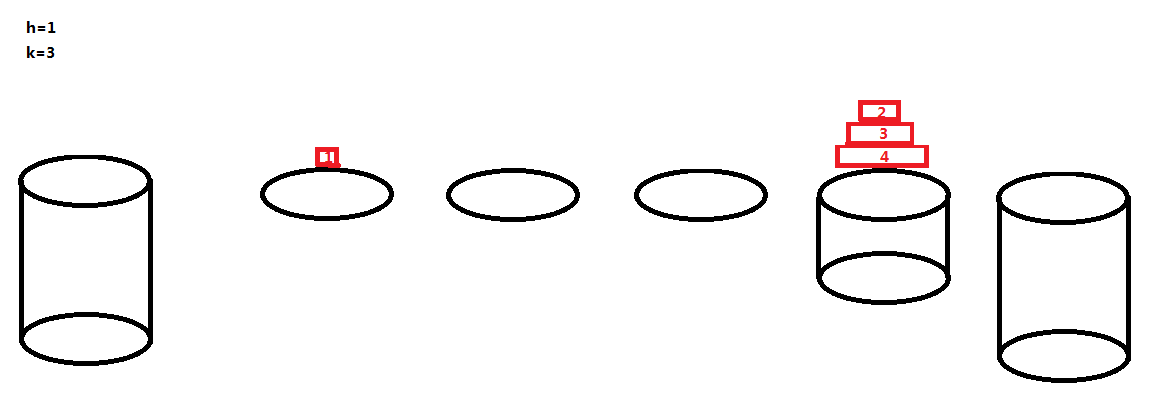
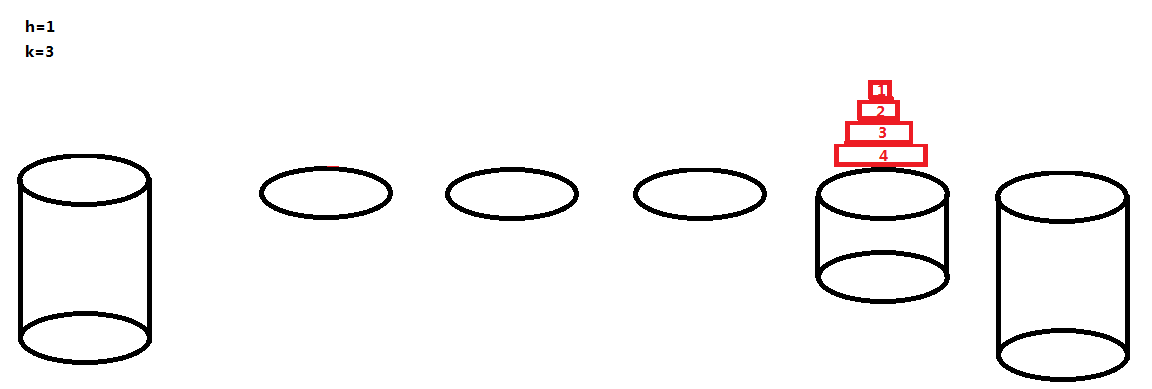
这一波操作之后,发现河中的这个石墩的最上面那只青蛙是 1,已经不能再往上跳青蛙了,我们可以暂且忽略这个石墩的存在了,那么河中只剩下了三个荷叶,也就是 h=0,k=3 的情况!
统计答案:
我们是先将河中石墩暂且看做是 h=0,k=3 情况下的石墩 B,那么这个石墩上最多载的青蛙就是 ans [ 0 ][ 3 ],然后剩下的就是 h=0,k=3 的情况了,那么又是一个 ans [ 0 ][ 3 ],最后的答案 ans [ 1 ][ 3 ] = ans [ 0 ][ 3 ] + ans [ 0 ][ 3 ] = 2 * ans [ 0 ][ 3 ];
按着这个思路,我们想一下 ans [ 2 ][ 3 ] 是多少:
也就是 h=1,k=3 的情况下又多了个石墩,那么我们把这个多的石墩看做是 h=1,k=3 情况下的石墩 B,那这个石墩上可以载的青蛙数就是 ans [ 1 ][ 3 ],这个石墩载满后,剩下的就是 h=1,k=3 的情况了,答案再加个 ans [ 1 ][ 3 ],最后的答案 ans [ 2 ][ 3 ] = ans [ 1 ][ 3 ] + ans [ 1 ][ 3 ] = 2 * ans [ 1 ][ 3 ];
由此我们可以发现:对于任何一个 h,k 的情况,我们都暂且可以把多出来的那个石墩看做是石墩 B,那么这个石墩上载的青蛙数最多为 ans [ h-1 ][ k ],这个石墩载满后,剩下的情况又是一个 ans [ h-1 ][ k ],则 ans [ h ][ k ] = ans [ h-1 ][ k ] + ans [ h-1 ][ k ] = 2 * ans [ h-1 ][ k ],这是个递归的过程;
因为河中多一个石墩答案就 ×2,所以也不难从中发现通项式:
ans [ h ][ k ] = 2h * k (相比于 h=0 的情况多了 h 个石墩,所以答案要乘 h 个 2,也就是 2h)
那么我们就可以愉快的 O ( 1 ) 出答案啦,超短代码如下:
#include<iostream> using namespace std; int h,k; int main() { cin>>h>>k; cout<<(1<<h)*(k+1); //注意h=0的情况下答案是k+1 }
Emmm,又是一道挂着 dp 标签的找规律题qwq