原题链接 https://www.luogu.com.cn/problem/P4462
题目大意
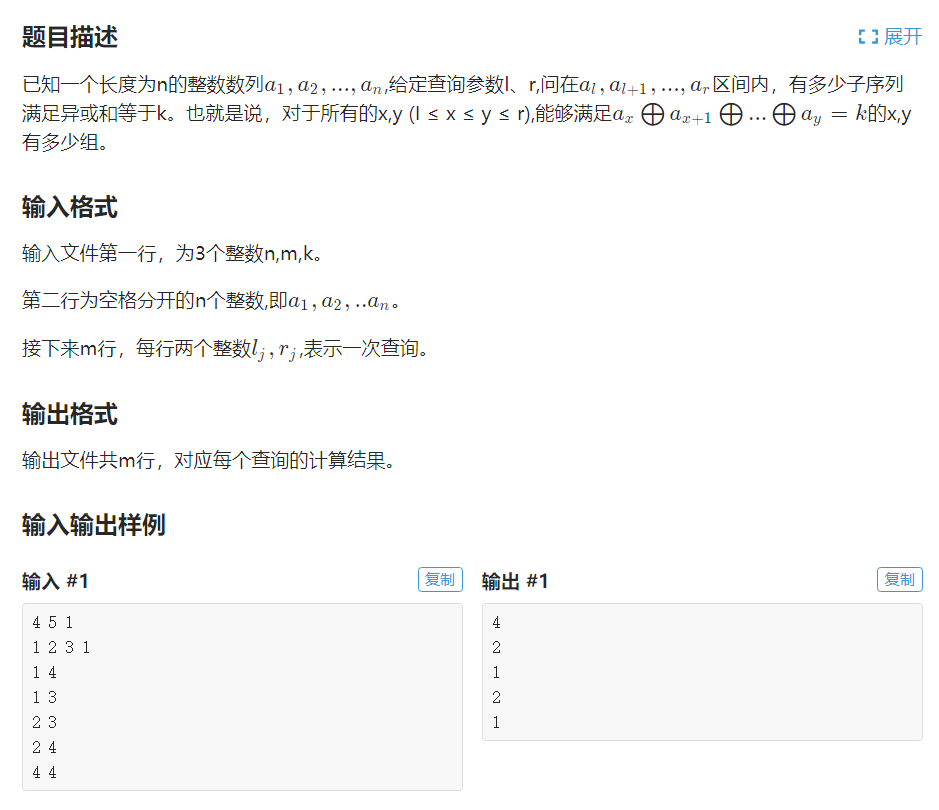
给你一个长度为 $n$ 的序列和 $m$ 次询问,求每次询问中有多少个子区间异或和为 $k$;
题解
这是一道区间查询的题目,所用的算法是数据结构,我这里用的是莫队算法;
回顾一下异或的神奇性质:
$1.a$ ^ $b = c$ ,则 $a$ ^ $ c = b$ ,$b$ ^ $c = a$ ;
$2. a$ ^ $a = 0$ ,$a$ ^ $0 = a$ ,则 $a$ ^ $a$ ^ $a = a$ ;
有了上面的性质,我们就可以把这一长串的异或化简一下了:
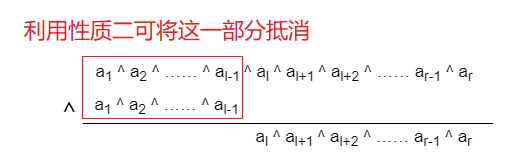
但是有些同学会问了:这不是更麻烦了嘛?怎么叫化简了呢?
我们可以用 $S_i$ 来表示区间 $[ 1,i ]$ 的异或和,即 $S_i = a_1$ ^ $a_2$ ^ $a_3$ …… ^ $a_i$ ;
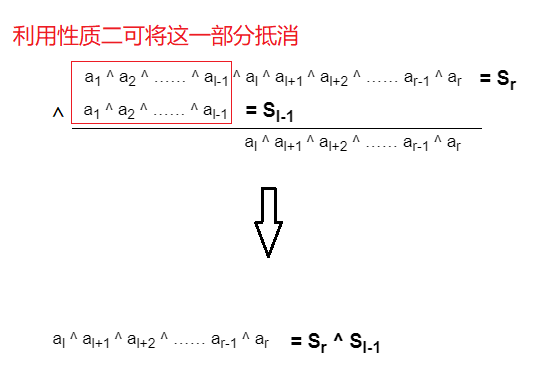
这样我们就将一串连续的数异或转化为了两个数的异或!
所以我们在求有多少个子区间时就是求有多少个 $S_j$ ^ $S_{i-1}= k ( l <= i <= j <= r )$ ;
接下来我们考虑区间转移对当前答案造成的影响:
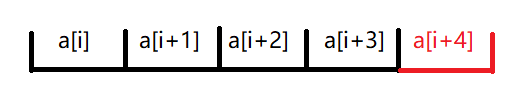
假如当前区间向右扩展了一个 $a [ i+4]$ ,那么它对答案造成的影响取决于以 $a [ i+4 ]$ 为结尾的若干区间中有多少个区间异或和为 $k$ ;
我们列举出所有以 $a [ i+4 ]$ 为结尾的区间:
$1. a [ i ]$ ^ $a [ i+1 ]$ ^ $a [ i+2 ]$ ^ $a [ i+3 ]$ ^ $ a [ i+4 ] = S_{i+4}$ ^ $S_{i-1} = k ?$
$2. a [ i+1 ]$ ^ $a [ i+2 ]$ ^ $a [ i+3 ]$ ^ $a [ i+4 ] = S_{i+4}$ ^ $S_i = k ?$
$3. a [ i+2 ]$ ^ $a [ i+3 ]$ ^ $a [ i+4 ] = S_{i+4}$ ^ $S_{i+1} = k ?$
$4. a [ i+3 ]$ ^ $a [ i+4 ] = S_{i+4}$ ^ $S_{i+1} = k ?$
$5. a [ i+4 ] = S_{i+4}$^ $S_{i+3} = k ?$
但是我们这样暴力搞的话时间复杂度不允许啊,莫队的每步转移都要控制在 $O (1)$ 的时间复杂度内;
想一想,如果有 $S_{i+4}$ ^ $S_x = k$ ,那么我们只需知道区间内有多少个异或前缀和为 $S_x$ ,答案就增加多少;
所以我们开一个数组 $times [ i ]$ 表示当前区间内有多少个异或前缀和为 $i$ ;
那么我们根据性质一可以得出:$S_x = S_{i+4}$ ^ $k$ ,所以答案会增加 $times [ S_{i+4}$ ^ $k ]$ ;
这样我们就 $O(1)$ 地解决了问题;
再看个例子:

假如当前区间的左端点向右转移了一个单位,那么我们要删除 $a [ i ]$ 对答案的影响,它对答案造成的影响取决于以 $a [ i ]$ 为开头的若干区间中有多少个区间异或和为 $k$ ;
我们列举出所有以 $a [ i ]$ 为开头的区间:
$1. a [ i ]$ ^ $a [ i+1 ]$ ^ $a [ i+2 ]$ ^ $a [ i+3 ]$ ^ $a [ i+4 ] = S_{i+4}$ ^ $S_{i-1} = k ?$
$2. a [ i ]$ ^ $a [ i+1 ]$ ^ $a [ i+2 ]$ ^ $a [ i+3 ] = S_{i+3}$ ^ $S_{i-1} = k ?$
$3. a [ i ]$ ^ $a [ i+1 ]$ ^ $a [ i+2 ] = S_{i+2}$ ^ $S_{i-1} = k ?$
$4. a [ i ]$ ^ $a [ i+1 ] = S_{i+1}$ ^ $S_{i-1} = k ?$
$5. a [ i ] = S_{i}$ ^ $S_{i-1} = k ?$
所以就是求有多少个 $S_x$ ^ $S_{i-1}= k$(注意这里是 $S_{i-1}$ 而不是 $S_i$ ),那么答案减少 $times [ S_{i-1}$ ^ $k ]$ ;
这里就是提醒大家在处理左端点时一定要注意 $-1$ 的问题,非常严重!(我就是这里卡了 $2h$
核心内容讲完了,剩下的就是一些莫队算法的内容了,建议不会莫队的童鞋先学会莫队再食用本代码哦~
$Code$:
#include<iostream> #include<algorithm> #include<cmath> #include<cstdio> using namespace std; long long read() { char ch=getchar(); long long a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } const long long N=1e5+5; long long n,m,k,nl=1,nr,len,num,ans; long long a[N],L[N],R[N],S[N],Ans[N],pos[N],times[N]; //times[i]:当前区间中异或和为i的前缀和有几个 struct node { long long l,r,id; }A[N<<2]; bool cmp(node x,node y) //奇偶性排序 { if(pos[x.l]!=pos[y.l]) return pos[x.l]<pos[y.l]; //若左端点不在同一块中,则左端点所在的块编号小的优先 if(pos[x.l]&1) return x.r<y.r; //若左端点在同一块中,且这个块的编号为奇数,则右端点小的优先 return x.r>y.r; //若这个块的编号为偶数,则右端点大的优先 } void add(long long x) //统计新增点a[x]的贡献 { ans+=times[S[x]^k]; //(S[x]^k)^S[x]=k times[S[x]]++; //当前区间内异或前缀和为S[x]的又多了一个 } void del(long long x) //删除点a[x]的贡献 { times[S[x]]--; //这里要先删除贡献 ans-=times[S[x]^k]; //然后在减去对答案的影响 } int main() { n=read();m=read();k=read(); for(long long i=1;i<=n;i++) { a[i]=read(); S[i]=S[i-1]^a[i]; //求异或前缀和 } len=num=sqrt(n); //每块的长度及要分成多少块 for(long long i=1;i<=num;i++) { L[i]=(i-1)*len+1; //每块的左端点 R[i]=i*len; //每块的右端点 for(long long j=L[i];j<=R[i];j++) pos[j]=i; //表示第j个数在第i个块里 } if(R[num]<n) //如果这些块不能包含所有的数,那么就再开一个块将剩下的数全放进去 { num++; //块数加一 L[num]=R[num-1]+1; R[num]=n; //这里右端点设为n,即序列的最后一个数 for(long long i=L[num];i<=R[num];i++) pos[i]=num; } for(long long i=1;i<=m;i++) //将m次询问的左右端点存下,待会离线处理 { A[i].l=read(); A[i].r=read(); A[i].id=i; //这是第几次询问 } sort(A+1,A+1+m,cmp); //将所有的块进行奇偶性排序 times[0]=1; //一开始当前区间没有任何元素 for(long long i=1;i<=m;i++) { while(nl<A[i].l) del(nl-1),nl++; //如果当前区间的左端点小于询问区间的左端点,则要删除该点的信息并向右转移 while(nl>A[i].l) nl--,add(nl-1); //如果当前区间的左端点大于询问区间的左端点,则要向左转移并统计新增点的信息 while(nr<A[i].r) add(++nr); //如果当前区间的右端点小于询问区间的右端点,则要向右转移并统计新增点的信息 while(nr>A[i].r) del(nr--); //如果当前区间的右端点大于询问区间的右端点,则要删除该点的信息并向左转移 Ans[A[i].id]=ans; //记录每次询问的答案,方便下面按询问顺序输出 } for(long long i=1;i<=m;i++) printf("%lld ",Ans[i]); //按照询问顺序输出答案 return 0; }