P6524题解

P6524 「Wdoi-1」托卡马克 题解

先前排声明一下,蒟蒻刚学OI没多久,而且是自学的,所以写的可能比较sb+累赘+表达不清楚

大致思路和上面那位dalao的差不多,有个错误也是看了上面那位dalao的题解才发现的qwq

大致题意

在n个点中选m个点进行两两相连,两个点相连所产生的费用为两点距离之差的绝对值
求严格第k大费用值(即不存在并列情况的第 k 大方案）

思路

先来看一下这个数据范围,k<=2

也就是说只有第一大和第二大两种可能

先来看一下k=1的时候的情况:

k=1

我们假设a1~a8是递增的,且n=8,m=6,k=1

先假设我们选取了(a_1),(a_2),(a_{3}),(a_{6}),(a_{7}),(a_{8})这几个数

总费用值=(sumlimits_{i=1,j=i+1}^{n-1,n}a_j-a_i)

通过观察可以发现有些值是可以进行拼接的

如(a_1)_{$a_8$=$a_1$}(a_3)+(a_3)_{$a_8$=$a_1$}(a_6)+(a_6)~(a_8)=...

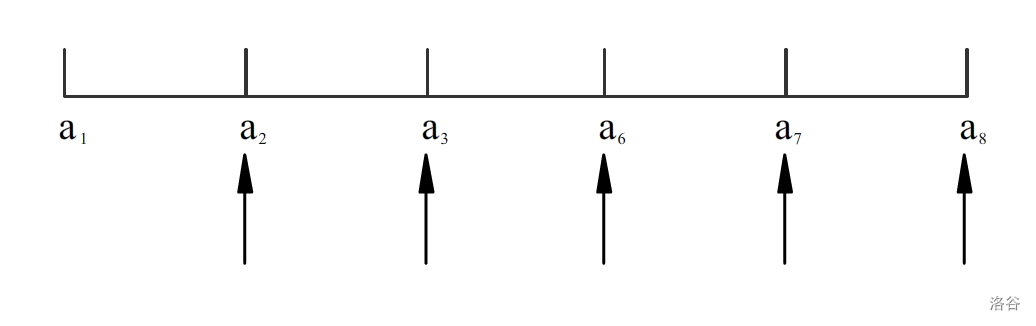
我们可以把这个拼接看成是在这一段的哪个位置断开

这样一轮下来就相当于把开头为1和结尾为8的所有段数全部加完了 这样我们就不用再考虑1和8了
可以将图简化成下面这个样子

(如图)

同样
(a_2)~(a_7)这段也一样,以此类推,直到缩小到不能再缩的时候停下就可以了

(大致过程)

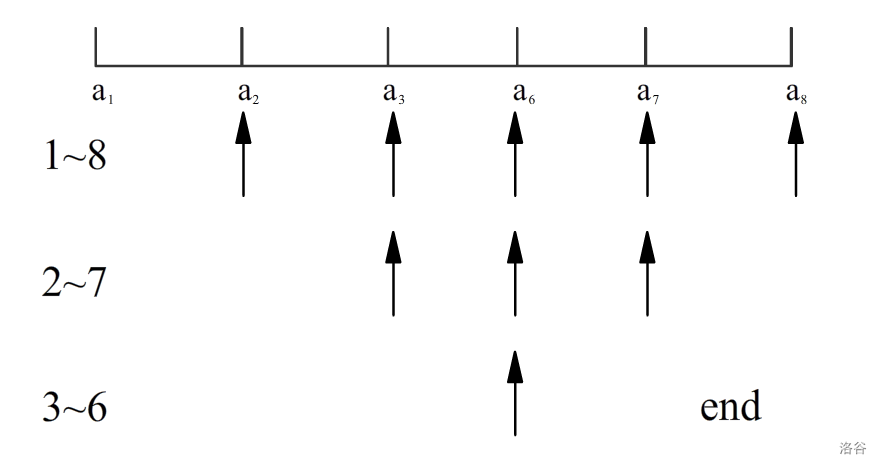
根据断点数量的规律

不难推出费用值=(sumlimits_{i=1}^frac{m}{2}(m-2(i-1)-1)*(a_{n-i+1}*a_i))

把((m-2(i-1)-1)*(a_{n-i+1}*a_i))看成一个组

根据贪心原则

当k=1时

每次只需要分别取原数列排序后最大和最小的两个值形成的组,即可

如图(n=8,m=6)

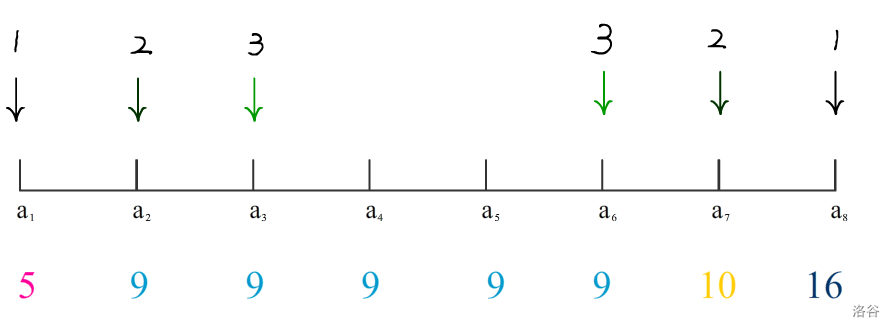
这样k=1的情况就做完了

下面来看k=2的情况

k=2

也就是次大的费用值

根据前面那个式子

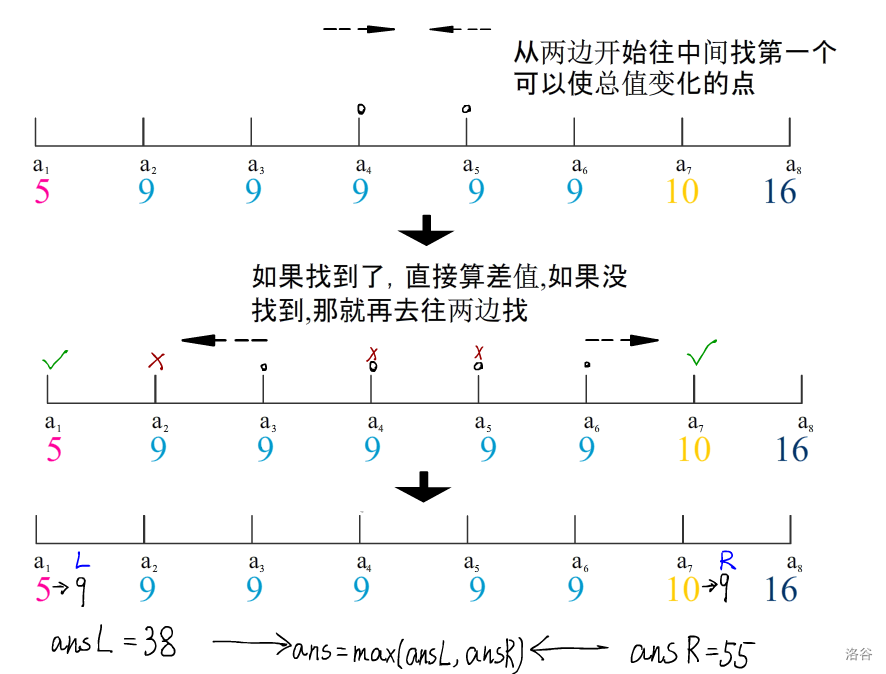
很明显可以看出,如果要得到次小费用值,就要取改变最靠近中间的那个点

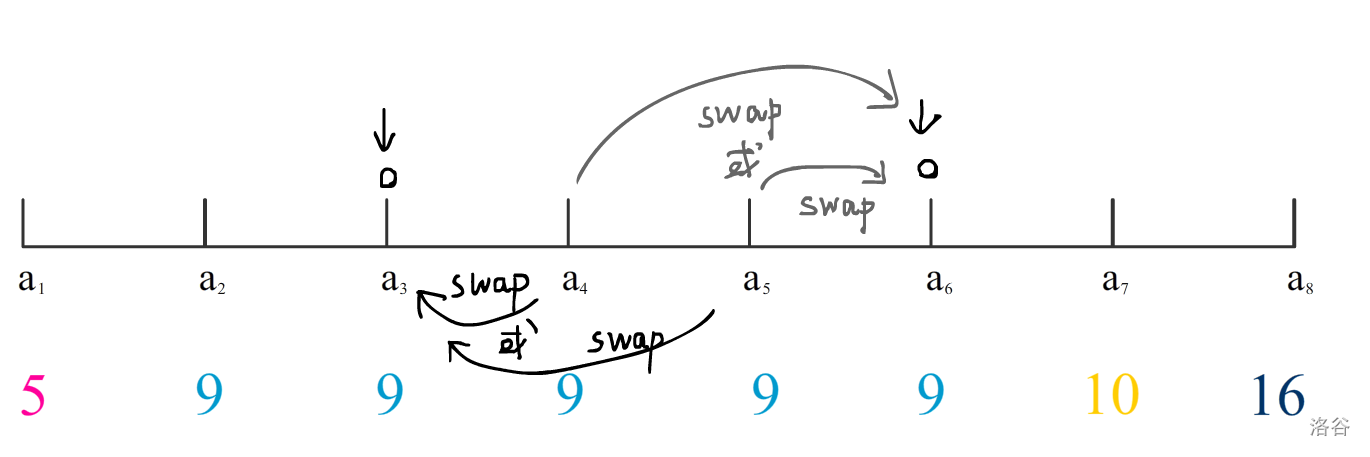
(左右两种方向)

但从图中的数据明显可以看出,当中间的所有值和最靠近中间的那个值相等时,是无法改变总数值的

因此在最靠中间的那个值无法对总数值进行改变时

就只能去考虑改变第二靠近中间的值了,以此类推

如果不管怎么移动都无法改变总数值

即各项均相等或n==m时

输出-1

贴上丑陋不堪的代码和大致流程图

#include<bits/stdc++.h>
using namespace std;
long long n,m,k,a[300010],ans,ansL,ansR;
int main(){
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	sort(a+1,a+n+1); 
	for(int i=1;i<=m/2;i++){
		ans+=(m-2(i-1)-1)*(a[n-i+1]-a[i]);//求第1大和
	}
	
	if(k==1) cout<<ans;
	else{
		if(n==m||a[1]==a[n]){
			cout<<-1;
			return 0;
		}
		for(int i=m/2+1;i<=n-m/2;i++){
			
			if(a[i]!=a[m/2]){
				ansL=a[i]-a[m/2];
				break;
			}
			
			if(i==n-m/2){
				
				for (int j=m/2-1;j>=1;j--) {
                    if (a[j]!=a[m/2]){	
                    	ansL=(m-2*j+1)*(a[m/2]-a[j]);//算差值
                    	break;
					}
                }
			}
		}
		
		for(int i=n-m/2;i>=m/2+1;i--){

			if(a[i]!=a[n-m/2+1]){
				ansR=a[n-m/2+1]-a[i];
				break;
			}
			if(i==m/2+1){
				
				for(int j=m/2+2;j<=n;j++){
					if (a[j]!=a[n-m/2+1]){
						
                    	ansR=(2*(j-n)+m-1)*(a[j]-a[n-m/2+1]);//化简了一下 
                    	break;
					}
				}
			}
		}
		cout<<max(ans-ansL,ans-ansR);
	}
}