Splay学习笔记

前置知识

二叉搜索树

一种二叉树的树形数据结构，其定义如下：

• 左子树上的所有节点的权值均小于其根节点的权值

• 右子树上的所有节点的权值均大于其根节点的权值

• 二叉搜索树的左右子树均为二叉搜索树

Splay

简介

一种自平衡二叉搜索树，通过不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质，且保持平衡而不至于退化为链

维护的信息

(root)	(tot)	(fa[i])	(child[i][0/1])	(val[i])	(cnt[i])	(size[i])
根节点	节点总数	父亲	左右儿子	点权	出现次数	子树大小

基本操作

• (update(x)) 更新(x)节点的(size)

• (clear(x)) 摧毁节点(x)

• (get(x)) 判断(x)是其父亲的左儿子还是右儿子

(code)

void clear(int x){child[x][0] = child[x][1] = size[x] = fa[x] = val[x] = 0;}
	void update(int x){if(!x) return; size[x] = size[child[x][0]]+size[child[x][1]]+1;}
	int get(int x){return x==child[fa[x]][1];}

• 旋转

为调换(Splay)中父子节点的位置,我们使用旋转操作,将一个节点向上移动一个位置,并保证:

• 整棵(Splay)的中序遍历不变

• 受影响的节点维护的信息依然正确有效

• (root)必须指向旋转后的根节点

具体步骤

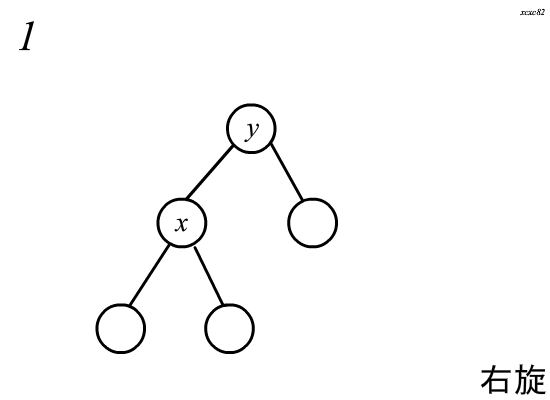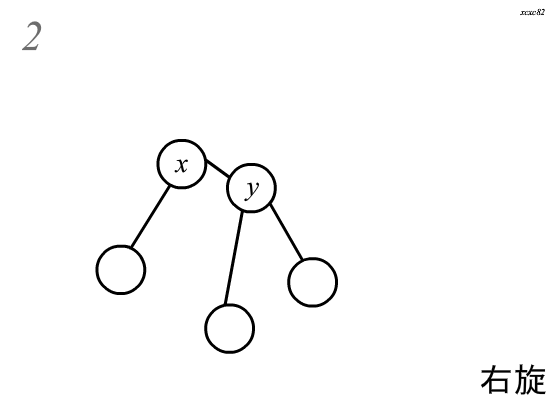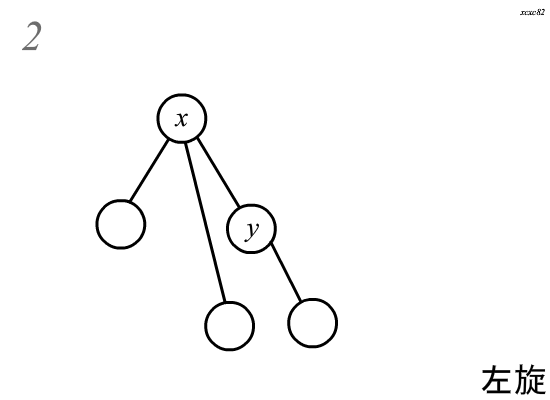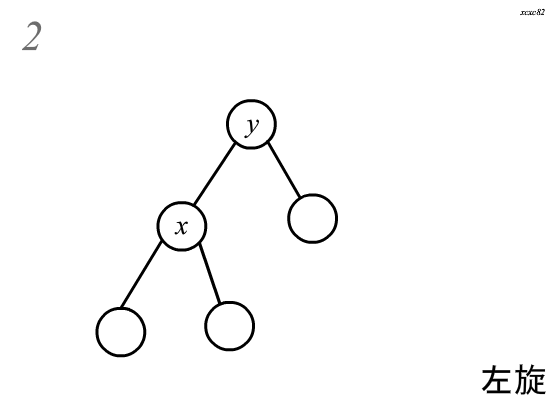
(Splay)中的旋转分为两种,左旋和右旋,这里以右旋为例:

旋转分为四个步骤(:)

(假设需要旋转的节点为(x),其父亲为(y))

(1.)将(y)的左儿子指向(x)的右儿子,且(x)的右儿子的父亲指向(y)

child[y][0] = child[x][1];
fa[child[x][1]] = y;

(2.)将(x)的右儿子指向(y)，且(y)的父亲指向(x)

child[x][1] = y;
fa[y] = x;

(3.)如果(y)还有父亲(z),将(y)原来在(z)中所在的位置指向(x),且(x)的父亲指向(y)

fa[x] = z;
child[z][y==child[z][1]] = x;

(4.)更新(x)和(y)的(size)

(code)

void rotate(int x){
		int y = fa[x],z=fa[y];
		int chy = get(x),chx = chy^1;
		child[y][chy] = child[x][chx];
		fa[child[x][chx]] = y;
		child[x][chx] = y;
		fa[y] = x;
		fa[x] = z;
		if(z) child[z][y==child[z][1]] = x;
		update(y),update(x);
	}

• (Splay)操作

(Splay)规定,每访问一个节点后,都要强制将该节点旋转到根的位置

具体步骤

为保证不退化成链,(Splay)操作一共分三步

(1.)如果父节点为目标位置,则向上旋转

(2.)如果当前节点与父节点的“关系”和父节点与祖父节点的“关系”相同，则先旋转父节点，再旋转自身

(3.)如果不满足以上条件,则将自身连续旋转两次

重复以上操作,直到旋转到根

(code)

void splay(int x,int goal){ 
    for (int f; (f=fa[x])!=goal; rotate(x)){
    	if (fa[f]!=goal) rotate(get(x)==get(f)?f:x);
	}
        
    if (!goal) root=x;
 }

• 插入

设插入的值为(k)

• 若树为空树,直接插入根

if(!root){
	val[++tot] = k;
	cnt[tot]++;
	root = tot;
	update(root);
	return;
}

• 否则,根据二叉搜索树的性质向下查找,直到查找到权值等于(k)的节点或空节点

同时需要将该节点(Splay)到根的位置

int now = root,f = 0;
	while(1){
		if(val[now]==k){
			cnt[now]++;
			update(now);
			update(f);
			Splay(now);
			break;
		}
		f = now;
		now = child[now][val[now]<k];
		if(!now){
			val[++tot] = k;
			cnt[tot]++;
			fa[tot] = f;
			child[f][val[f]<k] = tot;
			update(tot);
			update(f);
			Splay(tot);
			break;
		}
	}

• 排名

• 查询给定值的排名

设(x)为需要查询的值

根据二叉搜索树的性质:

• 若(x)比当前节点的权值小,向左子树查找

• 若(x)比当前节点的权值大，将答案(ans)加上左子树的(size)和当前节点(cnt)的大小,向其右子树查找。

• 若(x)与当前节点的权值相同,返回(ans+1)

(code)

int rank(int k){
	int ans = 0,now = root;
	while(1){
		if(k<val[now]) now = child[now][0];
		else{
			ans+=size[child[now][0]];
			if(k==val[now]){
				Splay(now);
				return ans+1;
			}
			ans+=cnt[now];
			now = child[now][1];
		}
	}
}

• 查询给定排名的值

设(k)为剩余排名,根据二叉搜索树的性质:

• 若(k)小于左子树的(size)且左子树非空,向左子树查找

• 否则将(k)减去左子树的大小和根的(cnt)

若此时(k)的值小于等于(0),返回根节点的权值

否则继续向右子树查找

(code)

int kth(int k){
  	int now = root;
  	while(1){
  		if(child[now][0]&&k<=size[child[now][0]]){
  			now = child[now][0];
  		}
  		else{
  			k-=cnt[now]+size[child[now][0]];
  			if(k<=0){
  				Splay(now);
  				return val[now];
  			}
  			now = child[now][1];
  		}
  	}
  }

• 前驱&&后继

一个数的前驱定义为小于(x)的最大的数

后继定义为大于(x)的最小的数

显然,一个数的前驱是其左子树中最靠右的节点,后继是其右子树的最靠左的节点

将(x)旋转到根后查询即可

(code)

int pre(){
   	  int now = child[root][0];
   	  while(child[now][1]) now = child[now][1];
   	  return now;
   }
   int next(){
   	int now = child[root][1];
   	while(child[now][0]) now = child[now][0];
   	return now;
   }

• 删除操作

首先将要删除的节点(x)旋转到根的位置

• 如果有不止一个(x),那么直接将(cnt[x])减(1)即可

否则

• 若没有儿子节点,直接将当前节点清空

• 若只有一个儿子,清空当前节点,再把根节点跟新为儿子

• 若有两个儿子,先将(x)的前驱旋转到根,并将(x)的右子树连接到(x)的前驱上

(code)

void del(int k){
		rank(k);
		if(cnt[root]>1){
			cnt[root]--;
			update(root);
			return;
		}
		if(!child[root][0]&&!child[root][1]){
			clear(root);
			root = 0;
			return;
		}
		if(!child[root][0]){
			int now = root;
			root = child[root][1];
			fa[root] = 0;
			clear(now);
			return;
		}
		if(!child[root][1]){
			int now = root;
			root = child[root][0];
			fa[root] = 0;
			clear(now);
			return;
		}
		int now = root,x = pre();
		fa[child[now][1]] = x;
		child[x][1] = child[now][1];
		clear(now);
		update(root);
		
	}

代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
int child[MAXN][2],size[MAXN],root,tot,fa[MAXN],val[MAXN],cnt[MAXN];
#define ci(Q) scanf("%d",&Q)
struct splay{
	void update(int x){size[x] = size[child[x][0]]+size[child[x][1]]+cnt[x];}
	bool pd(int x){return x==child[fa[x]][1];}
	void clear(int x){fa[x] = child[x][0] = child[x][1] = size[x] = val[x] = cnt[x] = 0;}
	void rotate(int x){
		int y = fa[x] , z = fa[y];
		int chy = pd(x) ,chx = chy^1;
		child[y][chy] = child[x][chx];
		fa[child[x][chx]] = y;
		child[x][chx] = y,fa[y] = x,fa[x] = z;
		if(z) child[z][y==child[z][1]] = x;
		update(x),update(y);
	} 
	void Splay(int x){
		for(int f = fa[x];f=fa[x],f;rotate(x)){
			if(fa[f]) rotate(pd(x)==pd(f)?f:x);
		}
		root = x;
	}
	void insert(int k){
		if(!root){
			val[++tot] = k;
			cnt[tot]++;
			root = tot;
			update(root);
			return;
		}
		int now = root,f = 0;
		while(1){
			if(val[now]==k){
				cnt[now]++;
				update(now);
				update(f);
				Splay(now);
				break;
			}
			f = now;
			now = child[now][val[now]<k];
			if(!now){
				val[++tot] = k;
				cnt[tot]++;
				fa[tot] = f;
				child[f][val[f]<k] = tot;
				update(tot);
				update(f);
				Splay(tot);
				break;
			}
		}
	}
	int rank(int k){
		int ans = 0,now = root;
		while(1){
			if(k<val[now]) now = child[now][0];
			else{
				ans+=size[child[now][0]];
				if(k==val[now]){
					Splay(now);
					return ans+1;
				}
				ans+=cnt[now];
				now = child[now][1];
			}
		}
	}
	int kth(int k){
		int now = root;
		while(1){
			if(child[now][0]&&k<=size[child[now][0]]){
				now = child[now][0];
			}
			else{
				k-=cnt[now]+size[child[now][0]];
				if(k<=0){
					Splay(now);
					return val[now];
				}
				now = child[now][1];
			}
		}
	}
	int pre(){
		int now = child[root][0];
		while(child[now][1]) now = child[now][1];
		Splay(now);
		return now;
	}
	int next(){
		int now = child[root][1];
		while(child[now][0]) now = child[now][0];
		Splay(now);
		return now;
	}
	void del(int k){
		rank(k);
		if(cnt[root]>1){
			cnt[root]--;
			update(root);
			return;
		}
		if(!child[root][0]&&!child[root][1]){
			clear(root);
			root = 0;
			return;
		}
		if(!child[root][0]){
			int now = root;
			root = child[root][1];
			fa[root] = 0;
			clear(now);
			return;
		}
		if(!child[root][1]){
			int now = root;
			root = child[root][0];
			fa[root] = 0;
			clear(now);
			return;
		}
		int now = root,x = pre();
		fa[child[now][1]] = x;
		child[x][1] = child[now][1];
		clear(now);
		update(root);
		
	}
}tree;
int main(){
	int n,op,x;
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&op,&x);
		if(op==1) tree.insert(x);
		else if(op==2) tree.del(x);
		else if(op==3) printf("%d
",tree.rank(x));
		else if(op==4) printf("%d
",tree.kth(x));
		else if(op==5) tree.insert(x),printf("%d
",val[tree.pre()]),tree.del(x);
		else tree.insert(x),printf("%d
",val[tree.next()]),tree.del(x);
	}
	return 0;
}

文艺平衡树(Splay维护区间信息)

大致题意

给一个长度为(n)的序列,序列中第(a_i)项的初始值为(i)

有(m)次区间翻转操作,输出经过 (m) 次变换后的结果

分析

按点的编号建立一颗(Splay)

每次翻转时

先将(val = l-1)和(val = r+1)的节点分别转到根和根的儿子节点

根据(Splay)的性质,整颗树的中序遍历不变

因此只需要将(child[child[root][1]][0])下的所有子树交换

通过给打懒标记的方式来实现交换操作即可

(code)

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
const int inf = 114514191;
int child[MAXN][2],a[MAXN],size[MAXN],root,tot,fa[MAXN],val[MAXN],cnt[MAXN],tag[MAXN];
struct Splay{
	void pushdown(int x){
		if(!tag[x]) return;
		tag[child[x][1]]^=1;
		tag[child[x][0]]^=1;
		swap(child[x][1],child[x][0]);
		tag[x] = 0;
	}
	void update(int x){size[x] = size[child[x][0]]+size[child[x][1]]+cnt[x];}
	bool pd(int x){return x==child[fa[x]][1];}
	void clear(int x){fa[x] = child[x][0] = child[x][1] = size[x] = val[x] = cnt[x] = 0;}
	void rotate(int x){
		int y = fa[x] , z = fa[y];
		int chy = pd(x) ,chx = chy^1;
		child[y][chy] = child[x][chx];
		fa[child[x][chx]] = y;
		child[x][chx] = y,fa[y] = x,fa[x] = z;
		if(z) child[z][y==child[z][1]] = x;
		update(x),update(y);
	} 
	int build(int l,int r,int f){
		if(l>r) return 0;
		int mid = (l+r)>>1;
		int now = ++tot;
		fa[now] = f;
		cnt[now]++;
		val[now] = a[mid];
	    size[now]++;
	    child[now][0] = build(l,mid-1,now);
	    child[now][1] = build(mid+1,r,now);
	    update(now);
	    return now;
	}
	void splay(int x,int goal){ 
    for (int f; (f=fa[x])!=goal; rotate(x)){
    	if (fa[f]!=goal) rotate(pd(x)==pd(f)?f:x);
	}
    if (!goal) root=x;
 }
 int kth(int k){
		int now = root;
		while(1){
			pushdown(now);
			if(child[now][0]&&k<=size[child[now][0]]){
				now = child[now][0];
			}
			else{
				int t = cnt[now]+size[child[now][0]];
				if(k<=t){
					return now;
				}
				k-=t;
				now = child[now][1];
			}
		}
	}
 void reverse(int x,int y){
 	int l = kth(x-1),r = kth(y+1);
 	splay(l,0),splay(r,l);
 	int now = child[root][1];
 	now = child[now][0];
 	tag[now]^=1;
 }
 void dfs(int x){
 	pushdown(x);
 	if(child[x][0]) dfs(child[x][0]);
 	if(val[x]!=inf&&val[x]!=-inf) cout<<val[x]<<" ";
	 if(child[x][1]) dfs(child[x][1]); 
 }
}tree; 
int main(){
	int n,m;
	cin>>n>>m;
	a[1] = -inf,a[n+2] = inf;//给区间[1,n]的序列翻转
	for(int i=1;i<=n;i++) a[i+1] = i;
	root = tree.build(1,n+2,0);
	for(int i=1;i<=m;i++){
		int l,r;
		cin>>l>>r;
		tree.reverse(l+1,r+1);
	} 
	tree.dfs(root);
}

参考资料

splay-oi-wiki

Splay 学习笔记（一）-Menci