1.1 Vertex cover
例子:
U = { 1, 2, 3, 4, 5, 6, 7 }
Sa = { 3, 7 } Sb = { 2, 4 }
Sc = { 3, 4, 5, 6 } Sd = { 5 }
Se = { 1 } Sf= { 1, 2, 6, 7 }
k = 2(Sc和Sf可以覆盖完原集合U)
1.1.1 VERTEX-COVER ≤ P SET-COVER
Pf. Given a VERTEX-COVER instance G = (V, E) and k, we construct a
SET-COVER instance (U, S, k) that has a set cover of size k iff G has a
vertex cover of size k.
给你一个顶点覆盖我们一定可以构造出一个集合覆盖实列,集合覆盖的解K就是顶点覆盖的解K
Construction:
- Universe U = E.
- Include one subset for each node v ∈ V : Sv = {e ∈ E : e incident to v }.
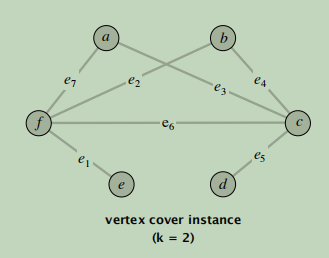
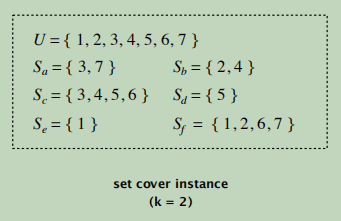
构造方法是这样的我们边的个数就等于集合U的大小,每一个结点邻接的边可表示为每一个独立子集比如结点f所连接的边为e1,e2,e6,e7.对应的子集和为{1,2,6,7}。
1.1.2 证明充分性
Pf. ⇒ Let X ⊆ V be a vertex cover of size k in G.
Then Y = { Sv : v ∈ X } is a set cover of size k.
“no” instances of VERTEX-COVER are solved correctly!
X为一个结点覆盖集合,那么是否一定可以找到对应的子集合?
一个实列:

如果我们选择f与c结点那么恰好可以对应到一个子集合覆盖。
但是如果我们顶点覆盖的点选择f和d,那么对应的子集合覆盖为Sf和sd显然这两个集合不能覆盖原集合U。
结论:无充分性!
1.1.3 证明必要性
Pf. ⇐ Let Y ⊆ S be a set cover of size k in (U, S, k).
- Then X = { v : Sv ∈ Y } is a vertex cover of size k in G.
“yes” instances of VERTEX-COVER are solved correctly!
由前面充分性失败的原因其实可以很好理解必要性是可以的!