二维数组最大子数和:
上一次挑战作业是一维数组中找最大子数和,难度不是很大,这一次变成了二维,且是一个矩阵,难度上升了一层。
题目简介:输入一个矩阵,从中找出最大的子数和(也为矩阵)。
解题思路:一开始没有想到有效的解决方法,但后面突然想到可以将二维数组变成一维数组来处理,简单来说,我们可以先搜寻矩阵中第一行的最大子数和,搜寻完后记录下来,然后寻找第一行每一列的数据,加上第二行每一列的数据,然后变成一个新的一维数组,又再次搜寻最大子数和,并和之前的子数和比较,取较大值,意思就是我们要把第i行和第i+n行的每一列数据加起来,变成一个新的一维数组,然后用寻找一维数组中的最大子数和的方法,去遍历所有可能性,这样的时间复杂度约为O(n^3)不算很大,可以自己去思考一下。
参考代码:
1 #include<bits/stdc++.h>
2 using namespace std;
3 #define MINX -100000
4 #define MAXN 10000
5 #define hang 3
6 #define lie 6
7
8 int Ywmaxarray(int * arr, int len) //找一维数组中最大子数和
9 {
10 int i, sum = arr[0], ans = 0;
11 for (i = 0; i < len; ++i)
12 {
13 if (ans>0)ans += arr[i];
14 else ans = arr[i];
15 if (ans>sum)sum = ans;
16 }
17 return sum;
18 }
19
20 int Ewmaxarray(int arr[hang][lie] ,int line , int column) //找二维数组中最大子数和
21 {
22 int k,ans=MINX;
23 int sum[MAXN];
24 for(int i = 0 ; i<line ; i++){memset(sum,0,sizeof(sum)); //sum为新的一维数组,每次使用前将其初始化
25 for(int j = i ; j < line ; j++ ){ //形成新的一维数组,并且传入到Ywmaxarray函数中去判断最大子数和
26 for(k = 0 ; k < column ; k ++){sum[k]+=arr[j][k];}
27 int maxs = Ywmaxarray(sum,k);
28 if(maxs>ans)
29 ans = maxs;
30 }
31 }
32 return ans;
33 }
34
35 int main( int argc , const char * argv[])
36 {
37 int num[hang][lie]={{5,6,-3, 8, -9, 2},
38 {1,-12,20,0,-3,-5},
39 {-9,-7,-3,6,7, -1}};
40 int answer = Ewmaxarray(num,hang,lie);
41 cout << answer << endl;
42 return 0;
43 }
为了方便观察,我直接将要判断的二维数组初始化赋值,每行每列的数字跟例题一样。
返回的最大子数和为28.
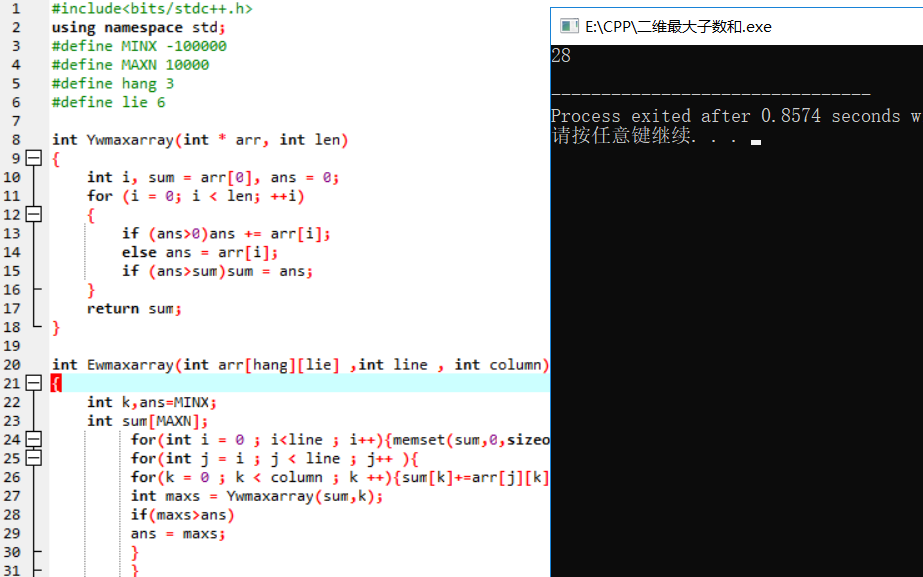
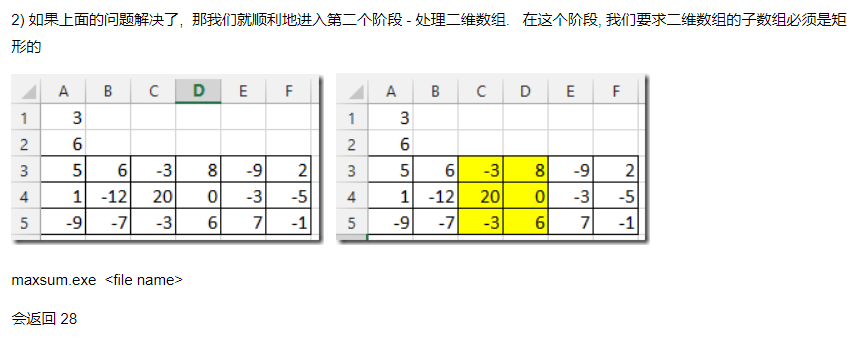
可以更改行列的值,然后初始化赋值相应行列,来观察其他二维数组的最大子数和,也可以直接改成输入,这里我就不改了,可以自己复制代码去改一改试试。

