对于灰度图而言,一个像素点由8个 bit 组成。代替突出灰度级范围,我们可以突出特定 bit 来为整个图像外观作出贡献,8 bit灰度图可考虑分层到 1-8 共8个比特平面。很容易理解的是,4个高阶比特平面,特别是最后两个比特平面,包含了在视觉上很重要的大多数数据。而低阶比特平面则在图像上贡献了更精细的灰度细节。
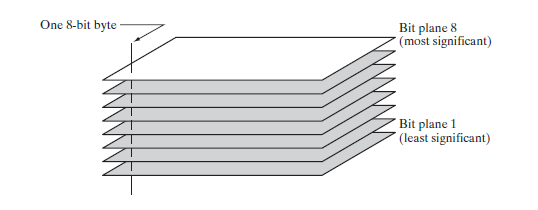
本篇博客在前面实现了灰度图的基础上,进一步探究 bit 平面分层的 FPGA 实现。由于Verilog中都是从0开始算起,所以bit平面我们定义为 0-7 层。
一、MATLAB实现
1 clear all; 2 3 RGB = imread('dollar.jpg'); %读取图片文件 4 5 gray = rgb2gray(RGB); %转换为灰度图像 6 [ROW,COL,N] = size(gray); %获得图片尺寸[高度,长度,维度] 7 8 subplot(3,3,1); 9 imshow(gray,[]); 10 title('原始图像'); 11 12 for k=1:8 13 for i=1:ROW 14 for j=1:COL 15 tmp(i,j) = bitget(gray(i,j),k);%将RGB(i,j)灰度值分解为二进制串,取第k位 16 end 17 end 18 subplot(3,3,k+1); 19 imshow(tmp,[]); 20 ind = num2str(k-1); 21 imti = ['第',ind,'个位平面']; 22 title(imti); 23 end
点击运行,得到如下结果:

二、FPGA实现
当看到 MATLAB 实现的代码时,我们会觉得如果用 Verilog 来实现会非常困难,其实不然,Verilog 是非常适合做这种运算的,关键代码如下所示:
assign bit_data_0 = {16{Y_data[0]}}; //0层 assign bit_data_1 = {16{Y_data[1]}}; //1层 assign bit_data_2 = {16{Y_data[2]}}; //2层 assign bit_data_3 = {16{Y_data[3]}}; //3层 assign bit_data_4 = {16{Y_data[4]}}; //4层 assign bit_data_5 = {16{Y_data[5]}}; //5层 assign bit_data_6 = {16{Y_data[6]}}; //6层 assign bit_data_7 = {16{Y_data[7]}}; //7层
其中 Y_data 是我们获得 YCbCr 格式的图像数据之后取出的 8 bit Y分量,即灰度数据。
由于FPGA编译综合、上板、传图,这一系列的操作实在过于繁琐,为了让实验更加简便,也为了能够更直观的对比各个层数的效果,我引入了一个外部按键。下载程序后初始层数为第0层,当按下按键时,层数会跟着转变,直到层数为第7层,之后按下按键又回到第0层,循环反复。
此外又引入了一个数码管显示模块,正好可以用来显示当前层数,不至于混淆,方便和MATLAB上的图案做对比。
本工程的整体模块如下所示:
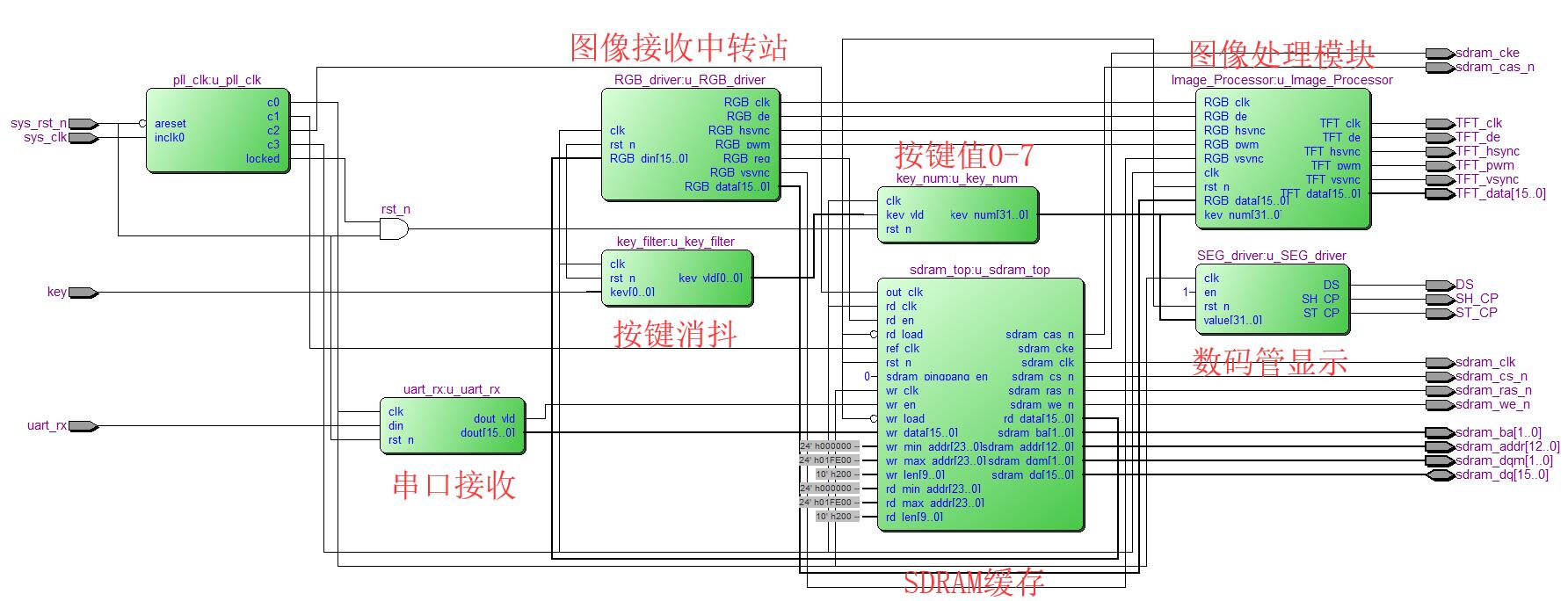
三、上板验证
唉我的板卡还是有问题,但这个实验是灰度图为基础,总体效果还行,就是背景本来应该是黑色,显示成了红色,糟心。
从视频可以看出,结果和我们的设计相符,各个层面的图像效果也和 MATLAB 做的一致,实验成功。
参考资料:
[1] OpenS Lee:FPGA开源工作室(公众号)
[2] https://blog.csdn.net/jzwong/article/details/52774393