决策树本质就是从训练数据集中归纳出一组分类规则,通过训练与数据集矛盾较小的决策树,同时具有较好的泛化能力。
通常该算法是一个递归的选择最优特征,并根据该特征对训练数据集进行分割,使得对各个子数据集具有较好的分类的过程。最开始将所有特征都放置在根结点,
选择最优特征,按照特征将训练集进行划分,使各子集在当前条件下分类效果(其中这个分类方法分别有:信息增益、gini值等)最佳,逐步递归分割结点,直到最终
所有的训练子集被分类到叶结点。如下图所示(x(1),x(2)分别表示每层筛选的最优分割特征):
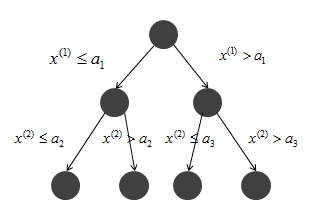
以上的方法对训练数据集能产生较好的拟合效果,然而对测试集的泛化能力并不一定如预期,因此有必要对生成树进行从上到下的剪枝,让树简化。具体就是通过去掉过于细分的
叶结点,并返回父结点或更高结点,再将父节点或更高的结点改为叶结点。
同时,如果数据集的特征过多,可以选择在一开始的时候就进行特征筛选,留下显著性特征再进行进一步的训练。
下面介绍用于特征筛选的方法:
(1)信息增益
首先介绍熵的概念,它是表示随机变量不确定性的度量,设X是一个取有限个值的离散随机变量,概率分布为:
P(X=xi)=pi i=1,2,.....,n
则随机变量X的熵定义为:
![]() (信息熵的3个性质:1)单调性 2)非负性 3)累加性)
(信息熵的3个性质:1)单调性 2)非负性 3)累加性)
在上式中,对数底选区2或e,分别对应熵的单位为bit或nat,由定义可以知道,熵只依赖于X的分布,而与X的取值无关,因此X的熵也可以记为H(p),因此式子也可表示为:
![]()
熵越大则随机变量的不确定性就越大,从定义可以验证:
![]()
当随机变量只取两个值如0,1时,X的分布为:
P(X=1)=p, P(X=0)=1-p, ![]()
则熵可以表示为:
H(p)=-plog2p-(1-p)log2(1-p)
上式在p的取值为0.5时熵最大,在p为0或1时,熵为0
设有随机变量(X,Y),其联合概率分布为
P(X=xi,Y=yi)=pij i=1,2,.....,n j=1,2,.....,m
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性,随即便利那个X给定条件下随机变量Y的条件熵H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望
![]()
其中,![]()
信息增益:
特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,表示为:
g(D,A)=H(D)-H(D|A)
一般情况下,熵H(Y)和条件熵H(Y|X)之差称为互信息,决策树学习的信息增益等价于训练数据集中类和特征的互信息。(互信息代表一个随机变量包含另一个随机变量信息量的度量,信息论中y的后验概率与先验概率比值的对数为x对y的互信息)
注(互信息的等价表示):
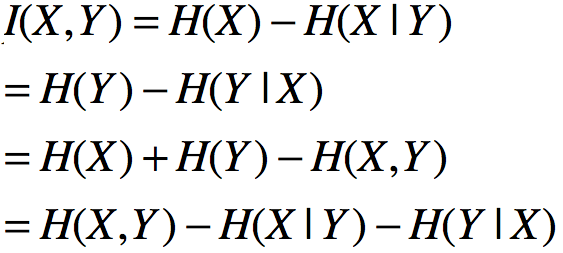
因此,有信息增益算法如下:
输入:训练数据集D和特征A
输出:特征A对训练数据集D的信息增益g(D,A)
(1)计算数据集D的经验熵H(D)
![]()
(2)计算特征A对数据集D的经验条件熵H(D|A)
![]()
(3)计算信息增益
g(D,A)=H(D)-H(D|A)
最终选取信息增益最大的特征作为筛选特征。(以上|D|表示数据集的样本容量,|Di|为划分后的样本数量,且各|Di|的和为|D|,|Ck|表示类|Ck|的样本数,子集Di中属于类Ck的样本集合为Dik)
经验熵H(D)表示对数据集D进行分类的不确定性,而经验条件熵H(D|A)表示在特征A给定的条件下对数据集D进行分类的不确定性,它们的差:信息增益,表示由于特征A使得数据集D的分类的不确定性减少的程度。