题目
如图,某物流派送员p,需要给a、b、c、d4个快递点派送包裹,请问派送员需要选择什么的路线,才能完成最短路程的派送。假设如图派送员的起点坐标(0,0),派送路线只能沿着图中的方格边行驶,每个小格都是正方形,且边长为1,如p到d的距离就是4。随机输入n个派送点坐标,求输出最短派送路线值(从起点开始完成n个点派送并回到起始点的距离)。
输入
4
2,2
2,8
4,4
7,2
输出30
输入
2,2
2,8
6,6
输出28
这个问题的条件比较特殊,不需要考虑实际送货中的特殊情况。
例如:实际生活中,有甲地,乙地和丙地。
情况1:若三地之间存在可直线行驶(或者较少绕路)的公路,则从甲地到丙地只需直走,若经由乙地到丙地会绕远(三角形任意两边之和大于第三边)。(只是一种理想情况,实际情况满足甲->丙->乙比甲->乙远都可归为此类)
情况2:若甲丙之间不存在可直线行驶(或者较少绕路)的公路,可以出现一种情况,就是甲地和丙地之间的交通很差()但是甲乙,乙丙直接交通较好,所以从甲到丙的最短路径经由乙。
分析该题目属于哪一种情况。
可以设三个点A(x1,y1),B(x2,y2),C(x3,y4),目的是A->C。
AC=|x1-x3|+|y1-y3|
AB+BC=|x1-x2|+|y1-y2|+|x3-x2|+|y3-y2|

所以|x1-x2|+|x3-x2|>=|(x1-x2)±(x3-x2)|
即|x1-x2|+|x3-x2|>=|x1-x3|且|x1-x2|+|x3-x2|>=|x1+x3-2x2|
同理|y1-y2|+|y3-y2|>=|y1-y3|且|y1-x2|+|y3-y2|>=|y1+y3-2y2|
所以|x1-x2|+|y1-y2|+|x3-x2|+|y3-y2| >=|x1-x3|+|y1-y3|
即AB+BC>=AC(同理AB+BD+DE+EF+……YZ+ZC>=AC)
所以在本题目中A->C必是一条最短路径。当且仅当x1<x2<x3,y1<y2<y3或者x1>x2>x3,y1>y2>y3,即B点位于ACx,y之间时等号成立,此时AB+BC=AC(AB+BD+DE+EF+……YZ+ZC=AC)但是AC仍然是最短路径之一。
当出现此条件是,可能会出现最短送货路径不止一条的情况,但一定有一条路径是回路的。
下面用图片的形式进行解释。
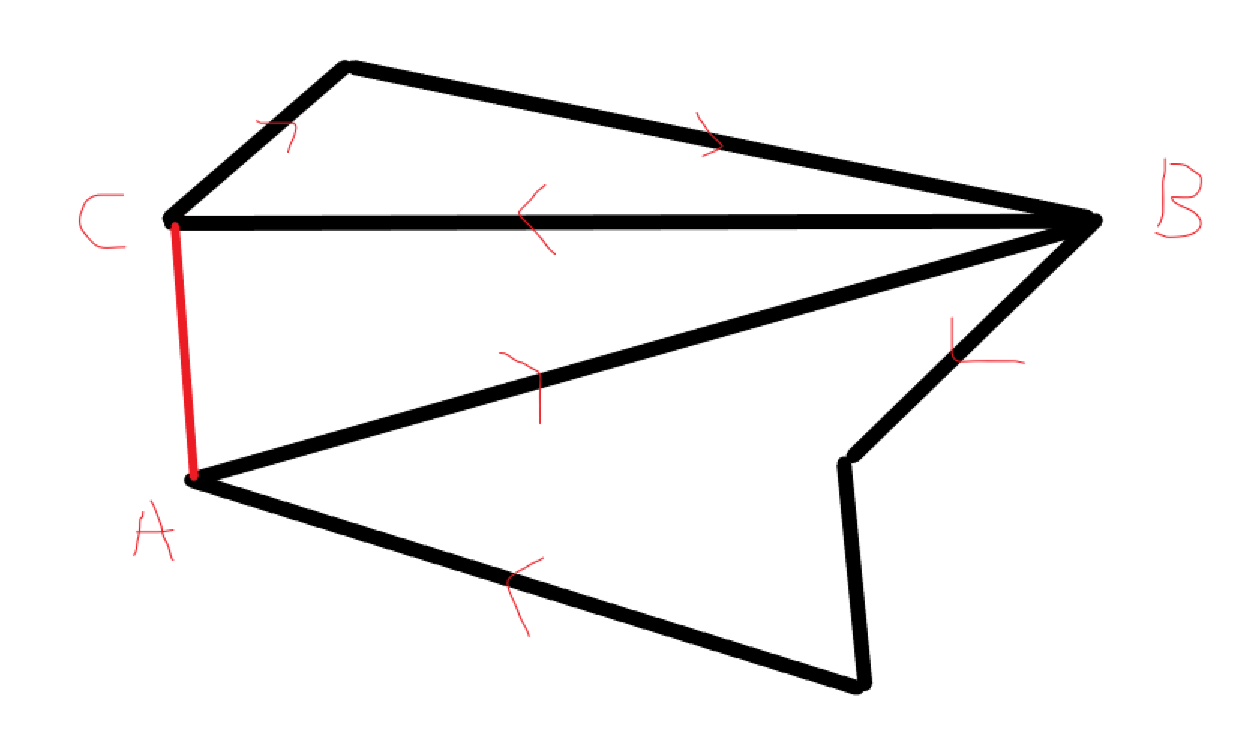
如图,假设一共有六个点,假设图中黑线是一条最短路径,有以上推论可以得出AC<=AB+BC那么AC也是一条最短路径且AB+BC=AC,此时B位于AC中间。
如果说B不满足这个条件那么原路径不是一条最短路径,应该是将A->B->C改为A->C的路径。所以无论ABC三点(AC之间也可以有多点,但原理相同)的相对
位置如何,必有一条A->C的路径为最短的。
所以此问题可以看作旅行商问题。
所以此问题可以看作旅行商问题。
所以此问题可以看作旅行商问题。
从原点出发将所有快递送达后回到原点。
