机器学习笔记-----牛顿法与拟牛顿法

提要：今天讲的牛顿法与拟牛顿法是求解无约束问题最优化方法的常用方法。

一 牛顿法

假设我们求下面函数的最小值：

假设f(x)具有连续的二阶的连续偏导数，假设第K次迭代值为x^k的值，那么可将f(X)在x^k附近进行二阶泰勒展开得到：

我们对上述公式求导可得:

    

假设其中可逆，我们就可以得到牛顿法的迭代公式为：

    

这样就可以得到牛顿法的迭代公式了。

牛顿法算法如下：

输入：目标函数f(X)，梯度▽f(x),海赛矩阵H(x),精度要求ε；

输出：f(x)的极小点x^*.

步骤一：取初始点x⁰,置k=0

步骤二：计算梯度▽f(x)

步骤三：||▽f(x)||〈ε，那么停止计算得到的x^*=x^k。

步骤四：计算H(x)

步骤五：

步骤6：转步骤二

牛顿法的缺点：牛顿法收敛速度快,但是要计算二阶偏导数矩阵及其逆阵,计算量过大。

二 拟牛顿法

拟牛顿法与原始牛顿法的区别在于增加了沿牛顿方向的一维搜索，其迭代公式为：

其中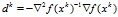为牛顿方向，是由一维搜索的步长，也就是满足：

    

其实牛顿法就是阻尼牛顿法步长为1的特殊情况。

拟牛顿法算法：

输入：目标函数f(X)，梯度▽f(x),海赛矩阵H(x),精度要求ε；

输出：f(x)的极小点x^*.

步骤一：取初始点x⁰,置k=0

步骤二：计算梯度▽f(x)

步骤三：||▽f(x)||〈ε，那么停止计算得到的x^*=x^k。

步骤四：计算H(x)

步骤五：从x^k出发，沿着d^k方向作一维搜索，

        

步骤六：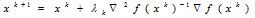

步骤七：转步骤二

本文完。